
【题目】为了提高学生阅读能力,我区某校倡议八年级学生利用双休日加强课外阅读,为了解同学们阅读的情况,学校随机抽查了部分同学周末阅读时间,并且得到数据绘制了不完整的统计图,根据图中信息回答下列问题:
(1)将条形统计图补充完整;被调查的学生周末阅读时间众数是多少小时,中位数是多少小时;
(2)计算被调查学生阅读时间的平均数;
(3)该校八年级共有500人,试估计周末阅读时间不低于1.5小时的人数.

【答案】(1)补全的条形统计图如图所示,见解析,被调查的学生周末阅读时间的众数是1.5小时,中位数是1.5小时;(2)所有被调查学生阅读时间的平均数为1.32小时;(3)估计周末阅读时间不低于1.5小时的人数为290人.
【解析】
(1)根据统计图可以求得本次调查的学生数,从而可以求得阅读时间1.5小时的学生数,进而可以将条形统计图补充完整;由补全的条形统计图可以得到抽查的学生周末阅读时间的众数、中位数.
(2)根据补全的条形统计图可以求得所有被调查学生阅读时间的平均数.
(3)用总人数乘以样本中周末阅读时间不低于1.5小时的人数占总人数的比例即可得.
解:(1)由题意可得,本次调查的学生数为:30÷30%=100,
阅读时间1.5小时的学生数为:100﹣12﹣30﹣18=40,
补全的条形统计图如图所示,
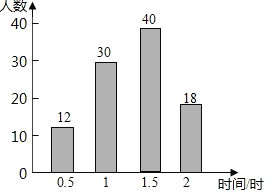
由补全的条形统计图可知,被调查的学生周末阅读时间众数是1.5小时,中位数是1.5小时,
故答案为:1.5,1.5;
(2)所有被调查学生阅读时间的平均数为:![]() ×(12×0.5+30×1+40×1.5+18×2)=1.32小时,
×(12×0.5+30×1+40×1.5+18×2)=1.32小时,
即所有被调查同学的平均阅读时间为1.32小时.
(3)估计周末阅读时间不低于1.5小时的人数为500×![]() =290(人).
=290(人).
故答案为:(1)补全的条形统计图如图所示,见解析,被调查的学生周末阅读时间的众数是1.5小时,中位数是1.5小时;(2)所有被调查学生阅读时间的平均数为1.32小时;(3)估计周末阅读时间不低于1.5小时的人数为290人.


 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:
【题目】如图1,已知直线y=﹣2x+4与两坐标轴分别交于点A、B,点C为线段OA上一动点,连接BC,作BC的中垂线分别交OB、AB交于点D、E.

(l)当点C与点O重合时,DE= ;
(2)当CE∥OB时,证明此时四边形BDCE为菱形;
(3)在点C的运动过程中,直接写出OD的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD=2,点E在边AD上(不与点A、D重合),∠CEB=45°,EB与对角线AC相交于点F,设DE=x.
(1)用含x的代数式表示线段CF的长;
(2)如果把△CAE的周长记作C△CAE,△BAF的周长记作C△BAF,设![]() =y,求y关于x的函数关系式,并写出它的定义域;
=y,求y关于x的函数关系式,并写出它的定义域;
(3)当∠ABE的正切值是![]() 时,求AB的长.
时,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进甲、乙两种商品,甲种商品共用了20000元,乙种商品共用了24000元.已知乙种商品每件进价比甲种商品每件进价多8元,且购进的甲、乙两种商品件数相同.
(1)求甲、乙两种商品的每件进价;
(2)该商场将购进的甲、乙两种商品进行销售,甲种商品的销售单价为60元,乙种商品的销售单价为88元,销售过程中发现甲种商品销量不好,商场决定:甲种商品销售一定数量后,将剩余的甲种商品按原销售单价的七折销售;乙种商品销售单价保持不变.要使两种商品全部售完后共获利不少于24600元,问甲种商品按原销售单价至少销售多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=3,BC=4,E,F是对角线AC上的两个动点,分别从A,C同时出发相向而行,速度均为1cm/s,运动时间为t秒,0≤t≤5.
(1)AE=________,EF=__________
(2)若G,H分别是AB,DC中点,求证:四边形EGFH是平行四边形.(![]() 相遇时除外)
相遇时除外)
(3)在(2)条件下,当t为何值时,四边形EGFH为矩形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填在相应的大括号里:
1,﹣![]() ,8.9,﹣7,
,8.9,﹣7, ![]() ,﹣3.2,+1 008,﹣0.06,28,﹣9.
,﹣3.2,+1 008,﹣0.06,28,﹣9.
正整数集合:{______…};
负整数集合:{______…};
正分数集合:{______…};
负分数集合:{______…}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名足球守门员练习折返跑,从球门的位置出发,向前记作正数,返回记作负数,他的记录如下(单位:米):
+6 | - 5 | +9 | - 10 | +13 | - 9 | - 4. |
(1)守门员是否回到了原来的位置?
(2)守门员离开球门的位置最远是多少?
(3)守门员一共走了多少路程?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“瓯柑”是温州的名优水果品牌。在平阳种植基地计划种植A、B两种瓯柑30亩,已知A、B两种瓯柑的年产量分别为2000千克/亩、2500千克/亩,收购单价分别是8元/千克、7元/千克.
(1)若该基地收获A、B两种瓯柑的年总产量为68000千克,求A、B两种瓯柑各种多少亩?
(2)若要求种植A种瓯柑的亩数不少于B种的一半,全部收购该基地瓯柑,那么种植A、 B两种瓯柑各多少亩时,其年总收入最多?最多为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,双边直尺有两条平行的边,但是没有刻度,可以用来画等距平行线:
![]()
我们也可用工具自制(如图):
![]()
下面是小My同学设计的“过直线外一点作这条直线的平行线”的双边直尺作图过程.
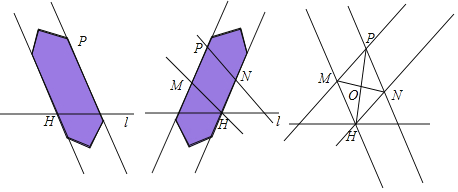
(1)根据小My同学的作图过程,请证明O为PH中点.
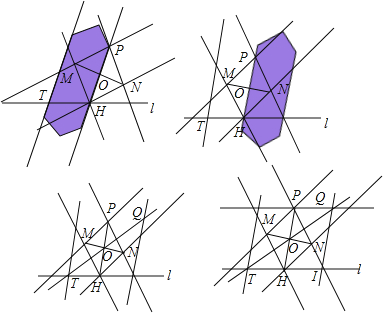
(2)根据小My同学的作图过程,请证明PQ∥l.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com