Question

【题目】在矩形ABCD中，AB＝3，BC＝4，E，F是对角线AC上的两个动点，分别从A，C同时出发相向而行，速度均为1cm/s，运动时间为t秒，0≤t≤5．

（1）AE＝________，EF＝__________

（2）若G，H分别是AB，DC中点，求证：四边形EGFH是平行四边形．（相遇时除外）

（3）在（2）条件下，当t为何值时，四边形EGFH为矩形．

Answer 1

【答案】（1）t， ；（2）详见解析；（3）当t为0.5秒或4.5时，四边形EGFH为矩形

【解析】

（1）先利用勾股定理求出AC的长度，再根据路程=速度×时间即可求出AE的长度，而当0≤t≤2.5时， ；当2.5＜t≤5时，即可求解；

（2）先通过SAS证明△AFG≌△CEH，由此可得到GF＝HE，，从而有，最后利用一组对边平行且相等即可证明；

（3）利用矩形的性质可知FG=EF,求出GH，用含t的代数式表示出EF,建立方程求解即可．

（1）

当0≤t≤2.5时，

当2.5＜t≤5时，

∴

故答案为：t，

（2）证明：∵四边形ABCD是矩形，

∴AB＝CD，AB∥CD，AD∥BC，∠B＝90°，

∴AC＝＝＝5，∠GAF＝∠HCE，

∵ G、H分别是AB、DC的中点，

∴AG＝BG，CH＝DH，

∴AG＝CH，

∵AE＝CF，

∴AF＝CE，

在△AFG与△CEH中，，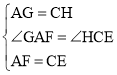

∴，

∴ GF＝HE，

∴四 边 形 EGFH是平行四边形．

（3）解：如图所示，连接GH，

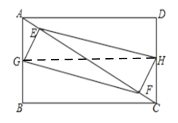
由（1）可知四边形EGFH是平行四边形

∵点 G、H分别是矩形ABCD的边AB、DC的中点，

∴ GH＝BC＝4，

∴ 当 EF＝GH＝4时，四边形EGFH是矩形，分两种情况：

①当0≤t≤2.5时,AE＝CF＝t，EF＝5﹣2t＝4，

解得：t＝0.5

②当2.5＜t≤5时，,AE＝CF＝t，EF＝2t-5＝4，

解得：t＝4.5

即：当t为0.5秒或4.5时，四边形EGFH为矩形