
【题目】如图1,在正方形ABCD中,对角线AC、BD交于点O,点E在AB上,点F在BC的延长线上,且AE=CF,连接EF交AC于点P,分别连接DE,DF,DP
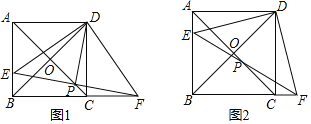
(1)求证:△ADE≌△CDF;
(2)求证:△ADP∽△BDF;
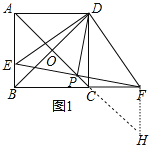
(3)如图2,若PE=BE,PC=![]() ,求CF的值.
,求CF的值.
【答案】(1)详见解析;(2)详见解析;(3)CF=![]() ﹣1,
﹣1,
【解析】
(1)根据SAS证明即可;
(2)如图1,作FH∥AB交AC的延长线于H.易证△APE≌△HPF(AAS),得PE=PF,再证△DEF是等腰直角三角形,得∠EDP=∠FDP=45°,进而得∠DAP=∠DBF,∠ADP=∠BDF即可得到结论;
(3)如图2,作PH⊥BC于H.首先证明∠EFB=30°,由PC=![]() ,得:HF=
,得:HF=![]() ,进而求出CF,即可解决问题.
,进而求出CF,即可解决问题.
(1)∵四边形ABCD是正方形,
∴DA=DC,∠DAE=∠BCD=∠DCF=90°,
∵AE=CF,
∴△ADE≌△CDF(SAS);
(2)如图1,作FH∥AB交AC的延长线于H.
∵四边形ABCD是正方形,
∴∠ACB=∠FCH=45°,
∵AB∥FH,
∴∠HFC=∠ABC=90°,
∴∠FCH=∠H=45°,
∴CF=FH=AE,
∵∠PAE=∠H=45°,∠APE=∠FPH,
∴△APE≌△HPF(AAS),
∴PE=PF,
∵△ADE≌△CDF,
∴DE=DF,∠ADE=∠CDF,
∴∠EDF=∠ADC=90°,
∴△DEF是等腰直角三角形,
∵EP=PF,
∴∠EDP=∠FDP=45°,
∵ADP=∠ADE+∠PDE=∠ADE+45°,∠BDF=∠CDF+∠BDC=∠CDF+45°,
∴∠ADP=∠BDF,
∵∠DAP=∠DBF=45°,
∴△ADP∽△BDF;
(3)如图2中,作PH⊥BC于H.
∵∠ACB=45°,PC=![]() ,
,
∴PH=CH=1.
由(2)得:BE=PE=PF,
∴BE=![]() EF,
EF,
∴∠BFE=30°,
∴PF=2,
∴HF=![]() ,
,
∴CF=![]() ﹣1,
﹣1,


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】将一个直角三角形纸片![]() 放置在平面直角坐标系中,已知点
放置在平面直角坐标系中,已知点![]() ,点
,点![]() ,点
,点![]() .
.![]() 是边
是边![]() 上的一动点(点
上的一动点(点![]() 不与点
不与点![]() 、
、![]() 重合),沿着
重合),沿着![]() 折叠该纸片,得点
折叠该纸片,得点![]() 的对应点
的对应点![]() .
.
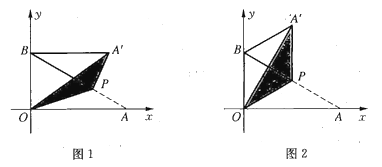
(1)如图1,当点![]() 在第一象限,且满足
在第一象限,且满足![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(2)如图2,当![]() 为
为![]() 中点时,求
中点时,求![]() 的长;
的长;
(3)当![]() 时,直接写出点
时,直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知两函数:反比例函数![]() 和二次函数y=
和二次函数y=![]() x2+x+a.
x2+x+a.
(1)若两个函数的图象都经过点(2,2).
①求两函数的表达式;
②证明反比例函数的图象经过二次函数图象的顶点.
(2)若二次函数y=![]() x2+x+a的图象与x轴有两个不同的交点,是否存在实数a,使方程
x2+x+a的图象与x轴有两个不同的交点,是否存在实数a,使方程![]() x2+x+a=0的两个实数根的倒数和等于﹣1?若存在,求出a的值;若不存在,说明理由.
x2+x+a=0的两个实数根的倒数和等于﹣1?若存在,求出a的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与x轴、y轴相交于P、Q两点,与
与x轴、y轴相交于P、Q两点,与![]() 的图象相交于
的图象相交于![]() 两点,连接OA,OB,给出下列结论:①
两点,连接OA,OB,给出下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④不等式
;④不等式![]() 的解集是
的解集是![]() 或
或![]() ,其中正确的是( )
,其中正确的是( )
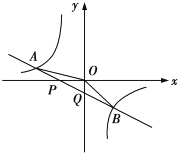
A.②③B.③④C.①②③④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4)
(1)请画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1;
(2)请画出△ABC关于原点O成中心对称的图形△A2B2C2;
(3)在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标.
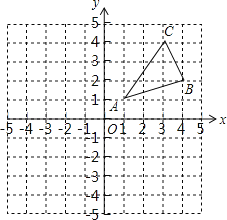
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4)
(1)请画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1;
(2)请画出△ABC关于原点O成中心对称的图形△A2B2C2;
(3)在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标.
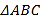
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课堂上,为了学习构成任意三角形三边需要满足的条件.甲组准备3根本条,长度分别是3cm、8cm、13cm;乙组准备3根本条,长度分别是4cm、6cm、12cm.老师先从甲组再从乙组分别随机抽出一根本条,放在一起组成一组.
(1)用画树状图法(或列表法)分析,并列出各组可能.(画树状图或列表及列出可能时不用写单位)
(2)现在老师也有一根本条,长度为5cm,与(1)中各组本条组成三角形的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
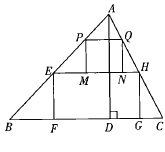
【题目】有一块锐角三角形卡纸余料ABC,它的边BC=120cm,高AD=80cm,为使卡纸余料得到充分利用,现把它裁剪成一个邻边之比为2:5的矩形纸片EFGH和正方形纸片PMNQ,裁剪时,矩形纸片的较长边在BC上,正方形纸片一边在矩形纸片的较长边EH上,其余顶点均分别在AB,AC上,具体裁剪方式如图所示。
(1)求矩形纸片较长边EH的长;
(2)裁剪正方形纸片时,小聪同学是按以下方法进行裁剪的:先沿着剩余料![]() 中与边EH平行的中位线剪一刀,再沿过该中位线两端点向边EH所作的垂线剪两刀,请你通过计算,判断小聪的剪法是否正确.
中与边EH平行的中位线剪一刀,再沿过该中位线两端点向边EH所作的垂线剪两刀,请你通过计算,判断小聪的剪法是否正确.
查看答案和解析>>
科目:初中数学 来源: 题型:
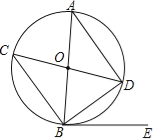
【题目】如图,在⊙O中,AB,CD是直径,BE是切线,B为切点,连接AD,BC,BD.
(1)求证:△ABD≌△CDB;
(2)若∠DBE=37°,求∠ADC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com