
【题目】将一个直角三角形纸片![]() 放置在平面直角坐标系中,已知点
放置在平面直角坐标系中,已知点![]() ,点
,点![]() ,点
,点![]() .
.![]() 是边
是边![]() 上的一动点(点
上的一动点(点![]() 不与点
不与点![]() 、
、![]() 重合),沿着
重合),沿着![]() 折叠该纸片,得点
折叠该纸片,得点![]() 的对应点
的对应点![]() .
.
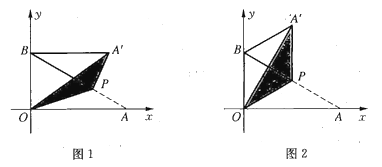
(1)如图1,当点![]() 在第一象限,且满足
在第一象限,且满足![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(2)如图2,当![]() 为
为![]() 中点时,求
中点时,求![]() 的长;
的长;
(3)当![]() 时,直接写出点
时,直接写出点![]() 的坐标.
的坐标.
科目:初中数学 来源: 题型:
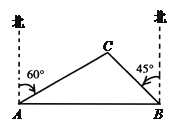
【题目】已知:如图,一艘渔船正在港口A的正东方向40海里的B处进行捕鱼作业,突然接到通知,要该船前往C岛运送一批物资到A港,已知C岛在A港的北偏东60°方向,且在B的北偏西45°方向.问该船从B处出发,以平均每小时20海里的速度行驶,需要多少时间才能把这批物资送到A港(精确到1小时)(该船在C岛停留半个小时)?(![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
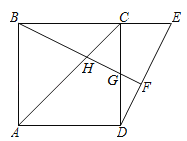
【题目】如图,点E是正方形ABCD的边BC延长线上一点,连结DE,过顶点B作BF⊥DE,垂足为F,BF分别交AC于H,交BC于G.
(1)求证:BG=DE;
(2)若点G为CD的中点,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
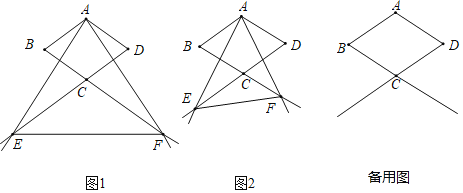
【题目】如图,菱形ABCD中,∠B=60°,AB=3cm,过点A作∠EAF=60°,分别交DC,BC的延长线于点E,F,连接EF.
(1)如图1,当CE=CF时,判断△AEF的形状,并说明理由;
(2)若△AEF是直角三角形,求CE,CF的长度;
(3)当CE,CF的长度发生变化时,△CEF的面积是否会发生变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
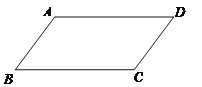
【题目】如图,已知AD∥BC,要使四边形ABCD为平行四边形,需要增加的一个条是:_____.(只填一个你认为正确的条件即可,不添加任何线段与字母)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为响应我市全民阅读活动,利用节假日面向社会开放学校图书馆.据统计,第一个月进馆128人次,进馆人次逐月增加,到第三个月末累计进馆608人次,若进馆人次的月平均增长率相同.
(1)求进馆人次的月平均增长率;
(2)因条件限制,学校图书馆每月接纳能力不超过500人次,在进馆人次的月平均增长率不变的条件下,校图书馆能否接纳第四个月的进馆人次,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 为正六边形
为正六边形![]() 的中心,点
的中心,点![]() 为
为![]() 中点,以点
中点,以点![]() 为圆心,以
为圆心,以![]() 的长为半径画弧得到扇形
的长为半径画弧得到扇形![]() ,点
,点![]() 在
在![]() 上,以点
上,以点![]() 为圆心,以
为圆心,以![]() 的长为半径画弧得到扇形
的长为半径画弧得到扇形![]() ,把扇形
,把扇形![]() 的两条半径
的两条半径![]() 重合,围成圆锥,将此圆锥的底面半径记为
重合,围成圆锥,将此圆锥的底面半径记为![]() ;将扇形
;将扇形![]() 以同样方法围成的圆锥的底面半径记为
以同样方法围成的圆锥的底面半径记为![]() ,则
,则![]() =______.
=______.
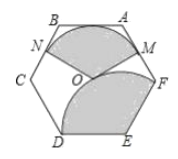
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点A是x轴上的一个动点,过点A作x轴的垂线PA交双曲线![]() 于点P,连接OP.
于点P,连接OP.
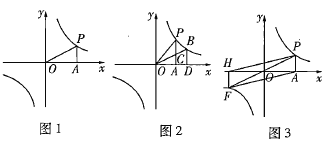
(1)当点A在x轴上的正方向上运动时,![]() 的面积是否发生变化?若不变,请求出
的面积是否发生变化?若不变,请求出![]() 的面积;若变化,请说明理由.
的面积;若变化,请说明理由.
(2)如图2,在x轴上点A的右侧有一点D,过点D作x轴的垂线DB交双曲线![]() 于点B,连接BO交AP于点C,设
于点B,连接BO交AP于点C,设![]() 的面积为
的面积为![]() ,梯形BCAD的面积为
,梯形BCAD的面积为![]() ,则
,则![]() 与
与![]() 的大小关系是
的大小关系是![]() ________
________![]() (选填“>”“=”或“<”)
(选填“>”“=”或“<”)
(3)如图3,PO的延长线与双曲线![]() 的另一个交点是F,作FH垂直于x轴,垂足为H,连接AF,PH,试说明四边形APHF的面积为常数.
的另一个交点是F,作FH垂直于x轴,垂足为H,连接AF,PH,试说明四边形APHF的面积为常数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,对角线AC、BD交于点O,点E在AB上,点F在BC的延长线上,且AE=CF,连接EF交AC于点P,分别连接DE,DF,DP
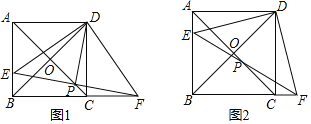
(1)求证:△ADE≌△CDF;
(2)求证:△ADP∽△BDF;
(3)如图2,若PE=BE,PC=![]() ,求CF的值.
,求CF的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com