

分析 (1)由待定系数法建立二元一次方程组求出m、n的值即可;
(2)先求出BC的解析式,设出点E的横坐标为a,由四边形CDBF的面积=S△BCD+S△CEF+S△BEF求出S与a的关系式,由二次函数的性质就可以求出结论.
(3)分两种情形讨论①当PD=DC时,当CP=CD时,分别写出点P坐标即可.
解答 解:(1)∵A(-1,0),C(0,2)在抛物线y=-$\frac{1}{2}$x2+mx+n上,
∴$\left\{\begin{array}{l}{n=2}\\{-\frac{1}{2}-m+2=0}\end{array}\right.$
∴$\left\{\begin{array}{l}{m=\frac{3}{2}}\\{n=2}\end{array}\right.$,
∴抛物线解析式为y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2.
(2)令y=0,则-$\frac{1}{2}$x2+$\frac{3}{2}$x+2=0,解得x=4或-1,
∴点B坐标(4,0),
设直线BC为y=kx+b,则$\left\{\begin{array}{l}{4k+b=0}\\{b=2}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=2}\end{array}\right.$,
∴直线BC解析式为y=-$\frac{1}{2}$x+2,
设出点E的横坐标为a
∴EF=Ey-Fy=-$\frac{1}{2}$a2+2a(0≤a≤4),
∴S四边形CDBF=S△BCD+S△CEF+S△BEF
=$\frac{1}{2}$BD×OC+$\frac{1}{2}$EF×CM+$\frac{1}{2}$EF×BN
=$\frac{1}{2}$×$\frac{5}{2}$×2+$\frac{1}{2}$×(-$\frac{1}{2}$a2+2a)×4
=-a2+4a+$\frac{5}{2}$
=-(a-2)2+$\frac{13}{2}$.
∴a=2时,四边形CDBF面积最大,此时点E坐标(2,1).
∴此时点E是BC中点,
∴当点E运动到BC中点时,四边形CDBF面积最大,最大面积为$\frac{13}{2}$,此时点E坐标(2,1).
(3)存在.
理由:∵C(0,2),D($\frac{3}{2}$,0),
∴CD=$\sqrt{{2}^{2}+(\frac{3}{2})^{2}}$=$\frac{5}{2}$,
①当PD=DC时,点P坐标($\frac{3}{2}$,$\frac{5}{2}$)或($\frac{3}{2}$,-$\frac{5}{2}$).
②当CP=CD时,点P坐标($\frac{3}{2}$,4),
③当CP=DP时,
设P($\frac{3}{2}$,n),
∴DP=|n|,CP=$\sqrt{\frac{9}{4}+(n-2)^{2}}$,
∴|n|=$\sqrt{\frac{9}{4}+(n-2)^{2}}$,
∴n=$\frac{25}{16}$,
∴P($\frac{3}{2}$,$\frac{25}{16}$)
∴当点P坐标($\frac{3}{2}$,$\frac{5}{2}$)或($\frac{3}{2}$,-$\frac{5}{2}$)或($\frac{3}{2}$,-4)或($\frac{3}{2}$,$\frac{25}{16}$)时,△PCD是以CD为腰的等腰三角形.
点评 此题是二次函数综合题,主要考查了待定系数法求一次函数的解析式的运用,二次函数的解析式的运用,勾股定理的运用,等腰三角形的性质的运用,四边形的面积的运用,解答时求出函数的解析式是关键.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
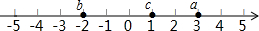 如图,数轴上有3个点,它们所表示的数分别用a,b,c.
如图,数轴上有3个点,它们所表示的数分别用a,b,c.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,一条信息可通过网络线由上(A点)往下(沿箭头方向)向各站点传送,例如信息要到b2点可由经a1的站点送达,也可由经a2的站点送达,共有两条传送途径,则信息由A点传达到d3的不同途径中,经过站点b3的概率为( )
如图,一条信息可通过网络线由上(A点)往下(沿箭头方向)向各站点传送,例如信息要到b2点可由经a1的站点送达,也可由经a2的站点送达,共有两条传送途径,则信息由A点传达到d3的不同途径中,经过站点b3的概率为( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | B. | 3$\sqrt{2}-\sqrt{2}$=2$\sqrt{2}$ | C. | 2$+\sqrt{2}=2\sqrt{2}$ | D. | $\sqrt{(-2)^{2}}$=±2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com