
【题目】魔术师把四张扑克牌放在桌子上,如图所示,然后蒙住眼睛,请一位观众上台把其中的一张处牌旋转180°放好,魔术师解开蒙着的眼睛的布后,看到四张牌如图23-2-8所示,他很快确定了被旋转的那一张牌,聪明的同学们,你知道哪一张牌被观众旋转过吗?说说你的理由.

 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
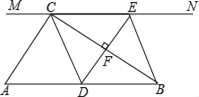
【题目】如图:在Rt△ABC中,∠ACB=90°,AB=6,过点C的直线MN∥AB,D为AB上一点,过点D作DE⊥BC,交直线MN于点E,垂足为F,连结CD,BE,
(1)当点D是AB的中点时,四边形BECD是什么特殊四边形?说明你的理由
(2)在(1)的条件下,当∠A= 时四边形BECD是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c过点A(0,2),且抛物线上任意不同两点M(x1,y1),N(x2,y2)都满足:当x1<x2<0时,(x1﹣x2)(y1﹣y2)>0;当0<x1<x2时,(x1﹣x2)(y1﹣y2)<0.以原点O为圆心,OA为半径的圆与抛物线的另两个交点为B,C,且B在C的左侧,△ABC有一个内角为60°.
(1)求抛物线的解析式;
(2)若MN与直线y=﹣2![]() x平行,且M,N位于直线BC的两侧,y1>y2,解决以下问题:
x平行,且M,N位于直线BC的两侧,y1>y2,解决以下问题:
①求证:BC平分∠MBN;
②求△MBC外心的纵坐标的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点.

(1)求该抛物线的解析式;
(2)求该抛物线的对称轴以及顶点坐标;
(3)设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足S△PAB=8,并求出此时P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD平分∠BAC,点P为线段AD上的一个动点,PE⊥AD交BC的延长线于点E.
(1)若∠B=35°,∠ACB=85°,求∠E得度数.
(2)当点P在线段AD上运动时,设∠B=α,∠ACB=β(β>α),求∠E得大小.(用含α、β的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 的周长是21,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=4, △ABC的面积是( )
的周长是21,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=4, △ABC的面积是( )

A.21B.42C.56D.84
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)如图所示,下列结论中:
①4ac-b2<0;②3b+2c<0;③4a+c<2b;④m(am+b)+b<a(m≠-1).
其中正确的结论有( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com