
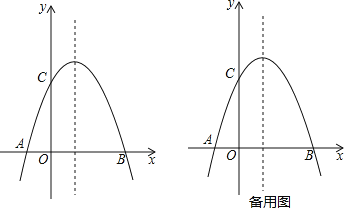
【题目】如图,已知抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,3).
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在点P,使得△PBC是等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由;
(3)连接CB,在直线CB上方的抛物线上有一点M,使得△BCM的面积最大,求出M点的坐标.
【答案】(1)![]() ;(2)共存在5个点P1(1,3+
;(2)共存在5个点P1(1,3+![]() ),P2(1,3-
),P2(1,3-![]() ),P3(1,
),P3(1,![]() ),P4(1,-
),P4(1,-![]() ),P5(1,1),使△PBC为等腰三角形;(3)M(
),P5(1,1),使△PBC为等腰三角形;(3)M(![]() ,
,![]() ).
).
【解析】
(1)利用待定系数法即可求得解析式;
(2)根据点P在抛物线对称轴上,可设点P的坐标为(1,m),分三种情况讨论,①PC=BC,②PB=BC,③PB=PC,求出m的值后即可得出答案.
(3)设M的坐标为(n,-n2+2n+3),根据S△BCM=S△OBC+S△OCM-S△OBC即可得出△BCM的面积S关于n的函数关系式,进而求得M的坐标.
:(1)设抛物线的解析式为y=ax2+bx+c,
∵抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,3).
∴  ,
,
解得, .
.
∴抛物线的解析式为y=-x2+2x+3;
(2)存在,理由如下:
∵抛物线与x轴交于A(-1,0)、B(3,0)两点,
∴抛物线的对称轴为:x=1,假设存在P(1,m)满足题意:
讨论:
①当PC=BC时,
∵OB=3,OC=3,
∴BC=3![]() ,
,
∴![]() ,
,
解得:m=3±![]() ,
,
∴P1(1,3+![]() ),P2(1,3-
),P2(1,3-![]() );
);
②当PB=BC时,![]() ,
,
解得:m3=![]() ,m4=-
,m4=-![]() ,
,
∴P3(1,![]() ),P4(1,-
),P4(1,-![]() ),
),
③当PB=PC时, ![]()
![]() ,
,
解得:m=1,
∴P5(1,1),
综上,共存在5个点P1(1,3+![]() ),P2(1,3-
),P2(1,3-![]() ),P3(1,
),P3(1,![]() ),P4(1,-
),P4(1,-![]() ),P5(1,1),使△PBC为等腰三角形.
),P5(1,1),使△PBC为等腰三角形.
(3)如图,设M的坐标为(n,-n2+2n+3),
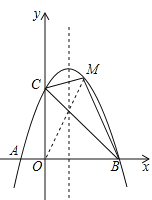
∵B(3,0),C(0,3).
∴OB=3,OC=3,
∴S△OBC=![]() ×3×3=
×3×3=![]() ,S△OBM=
,S△OBM=![]() ×3×(-n2+2n+3)=
×3×(-n2+2n+3)=![]() (-n2+2n+3),S△OCM=
(-n2+2n+3),S△OCM=![]() ×3×n=
×3×n=![]() n,
n,
∴S△BCM=S△OBM+S△OCM-S△OBC=![]() (-n2+2n+3)+
(-n2+2n+3)+![]() n-
n-![]() =-
=-![]() (n-
(n-![]() )2+
)2+![]() ,
,
∴当n=![]() 时,△BCM的面积最大,最大值是
时,△BCM的面积最大,最大值是![]() ,
,
∴M(![]() ,
,![]() ).
).


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
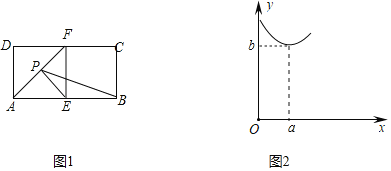
【题目】如图1,矩形ABCD中,AB=4,AD=2,E、F是边AB、DC的中点,连接EF、AF,动点P从A向F运动,AP=x,y=PE+PB.图2所示的是y关于x的函数图象,点(a,b)是函数图象的最低点,则a的值为( )
A.![]() B.
B.![]() C.
C.![]() D.2
D.2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,D是边AC上的一点,连接BD,使∠A=2∠1,E是BC上的一点,以BE为直径的⊙O经过点D.

(1)求证:AC是⊙O的切线;
(2)若∠A=60°,⊙O的半径为2,求阴影部分的面积.(结果保留根号和π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从淄博汽车站到银泰城有甲,乙,丙三条不同的公交线路.为了解早高峰期间这三条线路上的公交车从淄博汽车站到银泰城的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:
线路/公交车用时的频数/公交车用时 | 30≤t≤35 | 35≤t≤40 | 40≤t≤45 | 45≤t≤50 | 合计 |
甲 | 59 | 151 | 166 | 124 | 500 |
乙 | 50 | 50 | 122 | 278 | 500 |
丙 | 45 | 265 | 167 | 23 | 500 |
早高峰期间,乘坐线路上的公交车,从淄博汽车站到银泰城“用时不超过45分钟”的可能性最大.( )
A.甲B.乙C.丙D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在四边形ABCD中,AC⊥BD于点E,AB=AC=BD,点M为BC中点,N为线段AM上的点,且MB=MN.
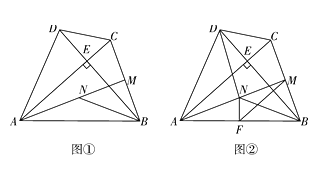
(1)求证:BN平分∠ABE;
(2)若BD=1,连结DN,当四边形DNBC为平行四边形时,求线段BC的长;
(3)如图②,若点F为AB的中点,连结FN、FM,求证:△MFN∽△BDC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,菱形![]() 中,
中,![]() ,垂足为
,垂足为![]() ,
,![]() ,
,![]() ,把四边形
,把四边形![]() 沿
沿![]() 所在直线折叠,使点
所在直线折叠,使点![]() 落在
落在![]() 上的点
上的点![]() 处,点
处,点![]() 落在点
落在点![]() 处,
处,![]() 交
交![]() 于点
于点![]() .
.


(1)证明:![]() ;
;
(2)求四边形![]() 面积;
面积;
(3)如图2,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 路径以每秒
路径以每秒![]() 的速度匀速运动,设运动时间为
的速度匀速运动,设运动时间为![]() 秒,当
秒,当![]() 为何值时,
为何值时,![]() 的面积与四边形
的面积与四边形![]() 的面积相等.
的面积相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
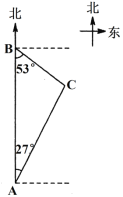
【题目】如图,海上有A、B、C三座小岛,小岛B在岛A的正北方向,距离为121海里,小岛C分别位于岛B的南偏东53°方向,位于岛A的北偏东27°方向,求小岛B和小岛C之间的距离.(参考数据:sin27°≈![]() ,cos27°≈
,cos27°≈![]() ,tan27°≈
,tan27°≈![]() ,sin53°≈
,sin53°≈![]() ,cos53°≈
,cos53°≈![]() ,tan53°≈
,tan53°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
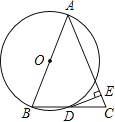
【题目】如图,以△ABC的一边AB为直径作⊙O,⊙O与BC边的交点恰好为BC的中点D,过点D作⊙O的切线交AC于点E.
(1)求证:DE⊥AC;
(2)若AB=3DE,求tan∠ACB的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com