
【题目】水利部确定每年的3月22日至28日为“中国水周”(1994年以前为7月1日至7日),从1991年起,我国还将每年5月的第二周作为城市节约用水宣传周.某社区为了进一步提高居民珍惜水、保护水和水忧患意识,提倡节约用水,从本社区5000户家庭中随机抽取100户,调查他们家庭每月的平均用水量,并将调查的结果绘制成如下的两幅不完整的统计图表:
用户月用水量频数分布表 | ||
平均用水量(吨) | 频数 | 频率 |
3~6吨 | 10 | 0.1 |
6~9吨 | m | 0.2 |
9~12吨 | 36 | 0.36 |
12~15吨 | 25 | n |
15~18吨 | 9 | 0.09 |

请根据上面的统计图表,解答下列问题:
(1)在频数分布表中:m=__ __,n=__ __;
(2)根据题中数据补全频数直方图;
(3)如果自来水公司将基本月用水量定为每户每月12吨,不超过基本月用水量的部分享受基本价格,超出基本月用水量的部分实行加价收费,那么该社区用户中约有多少户家庭能够全部享受基本价格?
【答案】(1)20,0.25;(2)补全频数分布直方图见解析;(3)该社区用户中约有3300户家庭能够全部享受基本价格.
【解析】
(1)根据频率=频数÷数据总数,可得到m÷100=0.2,可求得m=20,然后利用频率=频数÷数据总数可求得n的值;
(2)根据(1)中的结果画出频数分布直方图即可;
(3)求得100户家庭中能够全部享受基本价格的频数,然后再乘5000即可.
解:(1)m=100×0.2=20,n=25÷100=0.25.
(2)补全频数分布直方图如图:
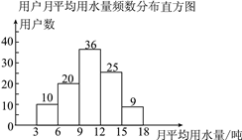
(3)![]() ×5000=3300(户).
×5000=3300(户).
所以该社区用户中约有3300户家庭能够全部享受基本价格.
故答案为:(1)20,0.25;(2)见解析;(3)3300户.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:
【题目】阅读下面材料:
数学活动课上,老师出了一道作图问题:“如图,已知直线l和直线l外一点P.用直尺和圆规作直线PQ,使PQ⊥l于点Q.”

小艾的作法如下:
(1)在直线l上任取点A,以A为圆心,AP长为半径画弧.
(2)在直线l上任取点B,以B为圆心,BP长为半径画弧.
(3)两弧分别交于点P和点M
(4)连接PM,与直线l交于点Q,直线PQ即为所求.
老师表扬了小艾的作法是对的.
请回答:小艾这样作图的依据是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,拦水坝的横断面为梯形ABCD,AB∥CD,坝顶宽DC为6米,坝高DG为2米,迎水坡BC的坡角为30°,坝底宽AB为(8+2 ![]() )米.
)米. 
(1)求背水坡AD的坡度;
(2)为了加固拦水坝,需将水坝加高2米,并且保持坝顶宽度不变,迎水坡和背水坡的坡度也不变,求加高后坝底HB的宽度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC,BD相交于点O,AE=CF.
(1)求证:△BOE≌△DOF;
(2)连接DE,BF,若BD⊥EF,试探究四边形EBFD的形状,并对结论给予证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等边△ABC,请用直尺(不带刻度)和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹): 
(1)作△ABC的外心O;
(2)设D是AB边上一点,在图中作出一个正六边形DEFGHI,使点F,点H分别在边BC和AC上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】雾霾天气已经成为人们普遍关注的话题,雾霾不仅仅影响人们的出行,还影响着人们的健康,太原市会持续出现雾霾天气吗?在2016年2月周末休息期间,某校九年级1班综合实践小组的同学以“雾霾天气的主要成因”为主题,随机调查了太原市部分市民的观点,并对调查结果进行了整理,绘制了如下不完整的统计图表,观察并回答下列问题:
类别 | 雾霾天气的主要成因 | 百分比 |
A | 工业污染 | 45% |
B | 汽车尾气排放 | m |
C | 城中村燃煤问题 | 15% |
D | 其他(绿化不足等) | n |

(1)请你求出本次被调查市民的人数及m,n的值,并补全条形统计图;
(2)若太原市有300万人口,请你估计持有A,B两类看法的市民共有多少人?
(3)学校要求小颖同学在A,B,C,D这四个雾霾天气的主要成因中,随机抽取两项作为课题研究的项目进行考察分析,请用画树状图或列表的方法,求出小颖同学刚好抽到B(汽车尾气排放),C(城中村燃煤问题)的概率.(用A,B,C,D表示各项目)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读与思考 婆罗摩笈多(Brahmagupta),是一位印度数学家和天文学家,书写了两部关于数学和天文学的书籍,他的一些数学成就在世界数学史上有较高的地位,他的负数概念及加减法运算仅晚于中国《九章算术》,而他的负数乘除法法则在全世界都是领先的,他还提出了著名的婆罗摩笈多定理,该定理的内容及部分证明过程如下:
已知:如图1,四边形ABCD内接于⊙O,对角线AC⊥BD于点P,PM⊥AB于点M,延长MP交CD于点N,求证:CN=DN.
证明:在△ABP和△BMP中,∵AC⊥BD,PM⊥AB,
∴∠BAP+∠ABP=90°,∠BPM+∠MBP=90°.
∴∠BAP=∠BPM.
∵∠DPN=∠BPM,∠BAP=∠BDC.
∴…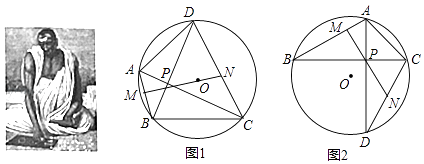
(1)请你阅读婆罗摩笈多定理的证明过程,完成剩余的证明部分.
(2)已知:如图2,△ABC内接于⊙O,∠B=30°,∠ACB=45°,AB=2,点D在⊙O上,∠BCD=60°,连接AD,与BC交于点P,作PM⊥AB于点M,延长MP交CD于点N,则PN的长为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com