
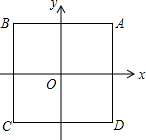
 如图,在坐标系中,点O是边长为2的正方形ABCD的中心,函数y=x2+c,使它的图象与正方形ABCD有公共点,则c的取值范围是-2≤c≤1.
如图,在坐标系中,点O是边长为2的正方形ABCD的中心,函数y=x2+c,使它的图象与正方形ABCD有公共点,则c的取值范围是-2≤c≤1.  寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:填空题
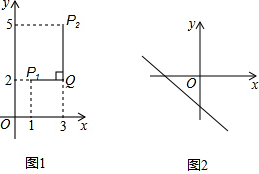 在平面直角坐标系xOy中,对于任意两点P1(x1,y1)与P2(x2,y2)的“非常距离”,给出如下定义:
在平面直角坐标系xOy中,对于任意两点P1(x1,y1)与P2(x2,y2)的“非常距离”,给出如下定义:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| x | … | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 10 | 5 | 2 | 1 | 2 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 基本事实和定理都是真命题 | |
| B. | 基本事实就是定理,定理就是基本事实 | |
| C. | 基本事实和定理都可以作为推理论证的依据 | |
| D. | 基本事实的正确性不需证明,定理的正确性需证明 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com