练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

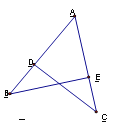
    【题目】如图：ΔABE≌ΔACD，AB=10cm，∠A=60°，∠B=30°，则AD=_____ cm，∠ADC=_____。

    【答案】5，90°

    【解析】试题分析：此题主要考查了全等三角形的性质，以及三角形内角和定理和直角三角形的性质，关键是掌握全等三角形的对应边相等，全等三角形的对应角相等．首先根据全等三角形的性质可得∠C=∠B=30°，AC=AB=10cm，再根据三角形内角和计算出∠ADC的度数，再根据直角三角形的性质可得AD=AC=5cm．

    解：∵△ABE≌△ACD，

    ∴∠C=∠B=30°，AC=AB=10cm，

    ∵∠A=60°，

    ∴∠ADC=180°-60°-30°=90°，

    ∴AD=AC=5cm，

    故答案为：5，90°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】(2016浙江省舟山市第19题)太阳能光伏建筑是现代绿色环保建筑之一，老张准备把自家屋顶改建成光伏瓦面，改建前屋顶截面△ABC如图2所示，BC=10米，∠ABC=∠ACB=36°，改建后顶点D在BA的延长线上，且∠BDC=90°，求改建后南屋面边沿增加部分AD的长．（结果精确到0.1米）

    （参考数据：sin18°≈0.31，cos18°≈0.95．tan18°≈0.32，sin36°≈0.59．cos36°≈0.81，tan36°≈0.73）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一元二次方程x2﹣x=0的根是

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列说法中，错误的是（　　）

    A. 两个全等三角形一定是相似形 B. 两个等腰三角形一定相似

    C. 两个等边三角形一定相似 D. 两个等腰直角三角形一定相似

    查看答案和解析>>

    科目：初中数学 来源： 题型：

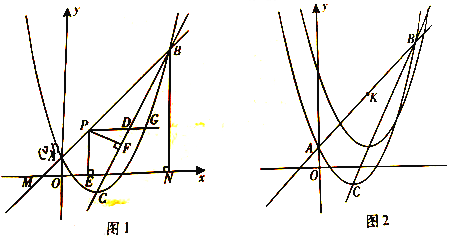
    【题目】(2016重庆市第26题)如图1，二次函数的图象与一次函数y=kx+b(k≠0)的图象交于A，B两点，点A的坐标为（0,1），点B在第一象限内，点C是二次函数图象的顶点，点M是一次函数y=kx+b(k≠0)的图象与x轴的交点，过点B作x轴的垂线，垂足为N，且S△AMO：S四边形AONB=1：48.

    （1）求直线AB和直线BC的解析式；

    （2）点P是线段AB上一点，点D是线段BC上一点，PD//x轴，射线PD与抛物线交于点G，过点P作PE⊥x轴于点E，PF⊥BC于点F，当PF与PE的乘积最大时，在线段AB上找一点H（不与点A，点B重合），使GH+BH的值最小，求点H的坐标和GH+BH的最小值；

    （3）如图2，直线AB上有一点K（3,4），将二次函数沿直线BC平移，平移的距离是t(t≥0)，平移后抛物线使点A，点C的对应点分别为点A’，点C’；当△A’C’K是直角三角形时，求t的值。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知：E是∠AOB的平分线上一点，EC⊥OB，ED⊥OA，C、D是垂足，连接CD，且交OE于点F.

    （1）求证：OE是CD的垂直平分线.

    （2）若∠AOB=60，请你探究OE，EF之间有什么数量关系？并证明你的结论。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点B和点C分别为∠MAN两边上的点，AB=AC.

    （1）按下列语句画出图形：(要求不写作法，保留作图痕迹)

    ① AD⊥BC，垂足为D；

    ② ∠BCN的平分线CE与AD的延长线交于点E；

    ③ 连结BE.

    （2）在完成（1）后不添加线段和字母的情况下，请你写出除△ABD≌△ACD外的两对全等三角形： ≌ ， ≌ ；并选择其中的一对全等三角形予以证明.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在墙壁上用两个钉子就能固定一根横放的木条，这样做根据的道理是（ ）

    A. 两点确定一条直线 B. 两点确定一条线段

    C. 两点之间，直线最短 D. 两点之间，线段最短

    查看答案和解析>>

    科目：初中数学 来源： 题型：

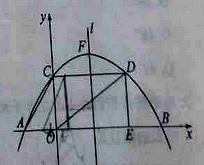
    【题目】(2016山东省聊城市第25题)如图，已知抛物线y=ax2+bx+c经过点A（﹣3，0），B（9，0）和C（0，4）．CD垂直于y轴，交抛物线于点D，DE垂直与x轴，垂足为E，l是抛物线的对称轴，点F是抛物线的顶点．

    （1）求出二次函数的表达式以及点D的坐标；

    （2）若Rt△AOC沿x轴向右平移到其直角边OC与对称轴l重合，再沿对称轴l向上平移到点C与点F重合，得到Rt△A1O1F，求此时Rt△A1O1F与矩形OCDE重叠部分的图形的面积；

    （3）若Rt△AOC沿x轴向右平移t个单位长度（0＜t≤6）得到Rt△A2O2C2，Rt△A2O2C2与Rt△OED重叠部分的图形面积记为S，求S与t之间的函数表达式，并写出自变量t的取值范围．

    查看答案和解析>>

    同步练习册答案