
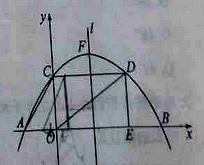
【题目】(2016山东省聊城市第25题)如图,已知抛物线y=ax2+bx+c经过点A(﹣3,0),B(9,0)和C(0,4).CD垂直于y轴,交抛物线于点D,DE垂直与x轴,垂足为E,l是抛物线的对称轴,点F是抛物线的顶点.
(1)求出二次函数的表达式以及点D的坐标;
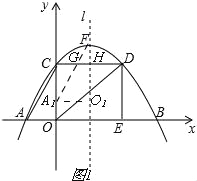
(2)若Rt△AOC沿x轴向右平移到其直角边OC与对称轴l重合,再沿对称轴l向上平移到点C与点F重合,得到Rt△A1O1F,求此时Rt△A1O1F与矩形OCDE重叠部分的图形的面积;
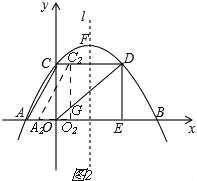
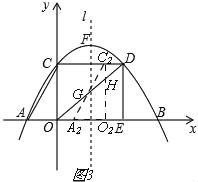
(3)若Rt△AOC沿x轴向右平移t个单位长度(0<t≤6)得到Rt△A2O2C2,Rt△A2O2C2与Rt△OED重叠部分的图形面积记为S,求S与t之间的函数表达式,并写出自变量t的取值范围.
【答案】(1)、D(6,4);y=﹣![]() x2+
x2+![]() x+4;(2)、
x+4;(2)、![]() ;(3)、当0<t≤3时,S=
;(3)、当0<t≤3时,S=![]() t2,当3<t≤6时,S=
t2,当3<t≤6时,S=![]() t2﹣3t+12
t2﹣3t+12
【解析】
试题分析:(1)、用待定系数法求抛物线解析式;(2)、由GH∥A1O1,求出GH=1,再求出FH,S重叠部分=S△A1O1F﹣S△FGH计算即可;(3)、分两种情况①直接用面积公式计算,②用面积差求出即可.
试题解析:(1)、∵抛物线y=ax2+bx+c经过点A(﹣3,0),B(9,0)和C(0,4).
∴设抛物线的解析式为y=a(x+3)(x﹣9), ∵C(0,4)在抛物线上, ∴4=﹣27a,
∴a=﹣![]() , ∴设抛物线的解析式为y=﹣
, ∴设抛物线的解析式为y=﹣![]() (x+3)(x﹣9)=﹣
(x+3)(x﹣9)=﹣![]() x2+
x2+![]() x+4,
x+4,
∵CD垂直于y轴,C(0,4) ∴﹣![]() x2+
x2+![]() x+4=4, ∴x=6, ∵D(6,4),
x+4=4, ∴x=6, ∵D(6,4),
(2)、如图1, ∵点F是抛物线y=﹣![]() x2+
x2+![]() x+4的顶点,∴F(3,
x+4的顶点,∴F(3,![]() ), ∴FH=
), ∴FH=![]() ,
,
∵GH∥A1O1, ∴![]() , ∴
, ∴![]() , ∴GH=1,
, ∴GH=1,
∵Rt△A1O1F与矩形OCDE重叠部分是梯形A1O1HG,
∴S重叠部分=S△A1O1F﹣S△FGH=![]() A1O1×O1F﹣
A1O1×O1F﹣![]() GH×FH=
GH×FH=![]() ×3×4﹣
×3×4﹣![]() ×1×
×1×![]() =
=![]() .
.
(3)、①当0<t≤3时,如图2, ∵C2O2∥DE, ∴![]() , ∴
, ∴![]() , ∴O2G=
, ∴O2G=![]() t,
t,
∴S=S△OO2G=![]() OO2×O2G=
OO2×O2G=![]() t×
t×![]() t=
t=![]() t2,
t2,
②当3<t≤6时,如图3, ∵C2H∥OC, ∴![]() , ∴
, ∴![]() , ∴C2H=
, ∴C2H=![]() (6﹣t),
(6﹣t),
∴S=S四边形A2O2HG=S△A2O2C2﹣S△C2GH=![]() OA×OC﹣
OA×OC﹣![]() C2H×(t﹣3)=
C2H×(t﹣3)=![]() ×3×4﹣
×3×4﹣![]() ×
×![]() (6﹣t)(t﹣3)=
(6﹣t)(t﹣3)=![]() t2﹣3t+12
t2﹣3t+12
∴当0<t≤3时,S=![]() t2,当3<t≤6时,S=
t2,当3<t≤6时,S=![]() t2﹣3t+12.
t2﹣3t+12.


科目:初中数学 来源: 题型:
【题目】如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC.将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE.则说明这两个三角形全等的依据是( )
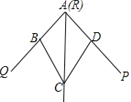
A. SAS B. ASA C. AAS D. SSS
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段AB,延长线段AB到点C,使![]() ,且BC比AB大1,D是线段AB的中点,如图所示.
,且BC比AB大1,D是线段AB的中点,如图所示.
![]()
(1)求线段CD的长;
(2)线段AC的长是线段DB的几倍?
(3)线段AD的长是线段BC的几分之几?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016山东省聊城市第17题)如图,在平面直角坐标系中,边长为1的正方形OA1B1C1的两边在坐标轴上,以它的对角线OB1为边作正方形OB1B2C2,再以正方形OB1B2C2的对角线OB2为边作正方形OB2B3C3,以此类推…、则正方形OB2015B2016C2016的顶点B2016的坐标是 .
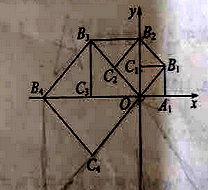
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班有48名同学,在一次英语单词竞赛成绩统计中,成绩在81~ 90这一分数段的人数所占的频率是0.25,那么成绩在这个分数段的同学有_________名.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com