
【题目】已知线段AB,延长线段AB到点C,使![]() ,且BC比AB大1,D是线段AB的中点,如图所示.
,且BC比AB大1,D是线段AB的中点,如图所示.
![]()
(1)求线段CD的长;
(2)线段AC的长是线段DB的几倍?
(3)线段AD的长是线段BC的几分之几?
【答案】(1)4; (2)5倍; (3)三分之一
【解析】试题分析:(1)设BC=3x,则AB=2x.因为BC比AB大1,可得3x-2x=1,解得x=1;即可得BC=3x=3,AB=2x=2.又因为D是线段AB的中点,所以AD=DB=1,所以CD=BC+BD=3+1=4;(2)根据AC=AB+BC求得AC的长,即可得线段AC与线段DB的数量关系;(3)根据AD、BC的长,即可得AD与BC的数量关系.
试题解析:
(1)因为BC=![]() AB,
AB,
所以BC∶AB=3∶2.
设BC=3x,则AB=2x.
因为BC比AB大1,所以3x-2x=1,即x=1,
所以BC=3x=3,AB=2x=2.
又因为D是线段AB的中点,所以AD=DB=1,
所以CD=BC+BD=3+1=4.
(2)因为AC=AB+BC=2+3=5,所以AC=5DB,即线段AC的长是线段DB的5倍.
(3)因为AD=1,BC=3,即3AD=BC,所以AD=BC,即线段AD的长是线段BC的三分之一.


 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案科目:初中数学 来源: 题型:
【题目】下列说法中,错误的是( )
A. 两个全等三角形一定是相似形 B. 两个等腰三角形一定相似
C. 两个等边三角形一定相似 D. 两个等腰直角三角形一定相似
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在墙壁上用两个钉子就能固定一根横放的木条,这样做根据的道理是( )
A. 两点确定一条直线 B. 两点确定一条线段
C. 两点之间,直线最短 D. 两点之间,线段最短
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图3,直线AB、CD相交于点O,∠AOE=90°,从给出的A、B、C三个答案中选择适当答案填空.

(1)∠1与∠2的关系是( )
(2)∠3与∠4的关系是( )
(3)∠3与∠2的关系是( )
(4)∠2与∠4的关系是( )
A.互为补角 B.互为余角 C.即不互补又不互余
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点C在线段AB上,线段AC=6厘米,BC=4厘米,点M,N分别是AC,BC的中点.
![]()
(1)求线段MN的长度;
(2)根据第(1)题的计算过程和结果,设AC+BC=a,其他条件不变,你能猜出MN的长度吗?请用一句话表述你发现的规律.
查看答案和解析>>
科目:初中数学 来源: 题型:
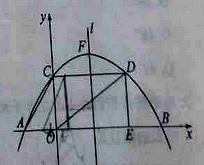
【题目】(2016山东省聊城市第25题)如图,已知抛物线y=ax2+bx+c经过点A(﹣3,0),B(9,0)和C(0,4).CD垂直于y轴,交抛物线于点D,DE垂直与x轴,垂足为E,l是抛物线的对称轴,点F是抛物线的顶点.
(1)求出二次函数的表达式以及点D的坐标;
(2)若Rt△AOC沿x轴向右平移到其直角边OC与对称轴l重合,再沿对称轴l向上平移到点C与点F重合,得到Rt△A1O1F,求此时Rt△A1O1F与矩形OCDE重叠部分的图形的面积;
(3)若Rt△AOC沿x轴向右平移t个单位长度(0<t≤6)得到Rt△A2O2C2,Rt△A2O2C2与Rt△OED重叠部分的图形面积记为S,求S与t之间的函数表达式,并写出自变量t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
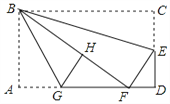
【题目】如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:① ∠EBG=45°;② AB : DE=AG : DF;③ S△ABG=![]() S△FGH;④ AG+DF=FG.其中正确的是_________.(填写正确结论的序号)
S△FGH;④ AG+DF=FG.其中正确的是_________.(填写正确结论的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com