
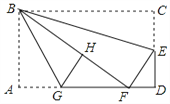
【题目】如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:① ∠EBG=45°;② AB : DE=AG : DF;③ S△ABG=![]() S△FGH;④ AG+DF=FG.其中正确的是_________.(填写正确结论的序号)
S△FGH;④ AG+DF=FG.其中正确的是_________.(填写正确结论的序号)
【答案】①③④
【解析】∵△BCE沿BE折叠,点C恰落在边AD上的点F处,∴∠1=∠2,CE=FE,BF=BC=10,
在Rt△ABF中,∵AB=6,BF=10,∴AF=![]() =8,∴DF=AD﹣AF=10﹣8=2,
=8,∴DF=AD﹣AF=10﹣8=2,
设EF=x,则CE=x,DE=CD﹣CE=6﹣x,在Rt△DEF中,∵DE2+DF2=EF2,∴(6﹣x)2+22=x2,解得x=![]() ,∴ED=
,∴ED=![]() ,
,
∵△ABG沿BG折叠,点A恰落在线段BF上的点H处,∴∠3=∠4,BH=BA=6,AG=HG,
∴∠2+∠3=![]() ∠ABC=45°,所以①正确;
∠ABC=45°,所以①正确;
HF=BF﹣BH=10﹣6=4,设AG=y,则GH=y,GF=8﹣y,
在Rt△HGF中,∵GH2+HF2=GF2,
∴y2+42=(8﹣y)2,解得y=3,∴AG=GH=3,GF=5,
∵∠A=∠D, 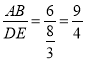 ,
, ![]() ,∴
,∴![]() ≠
≠![]() ,所以②错误;
,所以②错误;
∵S△ABG=![]() ×6×3=9,S△FGH=
×6×3=9,S△FGH=![]() GHHF=
GHHF=![]() ×3×4=6,
×3×4=6,
∴S△ABG=![]() S△FGH,所以③正确;
S△FGH,所以③正确;
∵AG+DF=3+2=5,而GF=5,∴AG+DF=GF,所以④正确.
故答案为①③④.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】用计算器计算数据13.49,13.53,14.07,13.51,13.84,13.98,14.67,14.80,14.61,14.60,14.41,14.31,14.38,14.02,14.17的平均数约为( )
A.14.15
B.14.16
C.14.17
D.14.20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段AB,延长线段AB到点C,使![]() ,且BC比AB大1,D是线段AB的中点,如图所示.
,且BC比AB大1,D是线段AB的中点,如图所示.
![]()
(1)求线段CD的长;
(2)线段AC的长是线段DB的几倍?
(3)线段AD的长是线段BC的几分之几?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班有48名同学,在一次英语单词竞赛成绩统计中,成绩在81~ 90这一分数段的人数所占的频率是0.25,那么成绩在这个分数段的同学有_________名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在由m×n(m×n>1)个小正方形组成的矩形网格中,研究它的一条对角线所穿过的小正方形个数f,
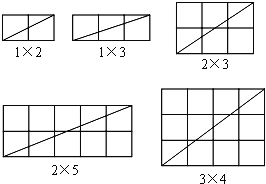
(1)当m、n互质(m、n除1外无其他公因数)时,观察下列图形并完成下表:
m | n | m+n | f |
1 | 2 | 3 | 2 |
1 | 3 | 4 | 3 |
2 | 3 | 5 | 4 |
2 | 5 | 7 | 6 |
3 | 4 | 7 | 6 |
猜想:当m、n互质时,在m×n的矩形网格中,一条对角线所穿过的小正方形的个数f与m、n的关系式是 (不需要证明);
(2)当m、n不互质时,请画图验证你猜想的关系式是否依然成立.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的三个顶点的坐标分别为A(﹣2,3)、B(﹣6,0),C(﹣1,0).
(1)将△ABC向右平移5个单位,再向下平移4个单位得△A1B1C1,图中画出△A1B1C1,平移后点A的对应点A1的坐标是______.
(2)将△ABC沿x轴翻折△A2BC,图中画出△A2BC,翻折后点A对应点A2坐标是______.
(3)将△ABC向左平移2个单位,则△ABC扫过的面积为______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com