
【题目】![]() 、
、![]() 两地在一直线上,且相距
两地在一直线上,且相距![]() ,甲、乙两人同时从
,甲、乙两人同时从![]() 、
、![]() 出发,分别沿射线
出发,分别沿射线![]() 、
、![]() 行进,其中甲的速度为
行进,其中甲的速度为![]() ,设他们出发
,设他们出发![]() 时,甲、乙两人离
时,甲、乙两人离![]() 地的距离分别为
地的距离分别为![]() 、
、![]() ,
,![]() 与
与![]() 的部分函数图象如图所示:
的部分函数图象如图所示:

(1)分别写出![]() ,
,![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)在所给的平面直角坐标系中画出(1)中的函数图象,直接写出![]() 、
、![]() 的图象交点坐标并解释其实际意义.
的图象交点坐标并解释其实际意义.
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
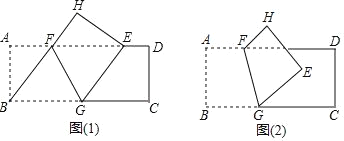
【题目】如图,长方形纸片ABCD中,AB=8,将纸片折叠,折痕的一个端点F在边AD上,另一个端点G在边BC上,顶点B的对应点为E.
(1)如图(1),当顶点B的对应点E落在边AD上时.
①连接BF,试判断四边形BGEF是怎样的特殊四边形,并说明理由;
②若BG=10,求折痕FG的长;
(2)如图(2),当顶点B的对应点E落在长方形内部,E到AD的距离为2,且BG=10时,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:关于x的二次函数![]() 的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
(1)求二次函数的表达式;
(2)在y轴上是否存在一点P,使△PBC为等腰三角形.若存在,请求出点P的坐标;
(3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到 达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的边OA在x轴上,将平行四边形沿对角线AC对折,AO的对应线段为AD,且点D,C,O在同一条直线上,AD与BC交于点E.

(1)求证:△ABC≌△CDA.
(2)若直线AB的函数表达式为![]() ,求三角线ACE的面积.
,求三角线ACE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=16cm,BC=6cm,动点P、Q分别以3cm/s,2cm/s的速度从点A,C同时出发,点Q从点C向点D移动.
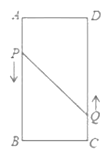
(1)设运动时间为![]() 秒,则AP= cm,DQ= cm;
秒,则AP= cm,DQ= cm;
(2)若点P从点A移动到点B停止,点Q随点P的停止而停止移动,点P,Q分别从点A,C同时出发,问经过多长时间P,Q两点之间的距离是10cm?
查看答案和解析>>
科目:初中数学 来源: 题型:
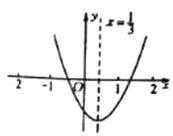
【题目】从如图所示的二次函数![]() 的图象中,观察得出下面五条信息:①
的图象中,观察得出下面五条信息:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() .你认为其中正确信息的个数为( )
.你认为其中正确信息的个数为( )
A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
丽丽这学期学习了轴对称的知识,知道了像角、等腰三角形、正方形、圆等图形都是轴对称图形.类比这一特性,丽丽发现像m+n,mnp,![]() 等代数式,如果任意交换两个字母的位置,式子的值都不变.太神奇了!于是她把这样的式子命名为神奇对称式.
等代数式,如果任意交换两个字母的位置,式子的值都不变.太神奇了!于是她把这样的式子命名为神奇对称式.
她还发现像![]() ,(m-1)(n-1)等神奇对称式都可以用
,(m-1)(n-1)等神奇对称式都可以用![]() 表示.例如:
表示.例如:![]() .于是丽丽把
.于是丽丽把![]() 称为基本神奇对称式 .
称为基本神奇对称式 .
请根据以上材料解决下列问题:
(1)代数式①![]() , ②
, ②![]() , ③
, ③![]() , ④ xy + yz + zx中,属于神奇对称式的是__________(填序号);
, ④ xy + yz + zx中,属于神奇对称式的是__________(填序号);
(2)已知![]() .
.
① q=__________(用含m,n的代数式表示);
② 若![]() ,则神奇对称式
,则神奇对称式![]() =__________;
=__________;
③ 若![]() ,求神奇对称式
,求神奇对称式![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以直角![]() 的斜边AB,直角边AC为边向
的斜边AB,直角边AC为边向![]() 外作等边
外作等边![]() 和等边
和等边![]() ,F为AB的中点,DE与AB交于点G,EF与AC交于点H,
,F为AB的中点,DE与AB交于点G,EF与AC交于点H,![]() ,
,![]() .给出如下结论:
.给出如下结论:
①EF⊥AC; ②四边形ADFE为菱形; ③![]() ; ④
; ④![]() ;
;
其中正确结论的是( )

A. ①②③B. ②③④C. ①③④D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某新型高科技商品,每件的售价比进价多6元,5件的进价相当于4件的售价,每天可售出200件,经市场调查发现,如果每件商品涨价1元,每天就会少卖5件.
(1)该商品的售价和进价分别是多少元?
(2)设每天的销售利润为w元,每件商品涨价x元,则当售价为多少元时,该商品每天的销售利润最大,最大利润为多少元?
(3)为增加销售利润,营销部推出了以下两种销售方案:方案一:每件商品涨价不超过8元;方案二:每件商品的利润至少为24元,请比较哪种方案的销售利润更高,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com