
【题目】阅读下面材料:
丽丽这学期学习了轴对称的知识,知道了像角、等腰三角形、正方形、圆等图形都是轴对称图形.类比这一特性,丽丽发现像m+n,mnp,![]() 等代数式,如果任意交换两个字母的位置,式子的值都不变.太神奇了!于是她把这样的式子命名为神奇对称式.
等代数式,如果任意交换两个字母的位置,式子的值都不变.太神奇了!于是她把这样的式子命名为神奇对称式.
她还发现像![]() ,(m-1)(n-1)等神奇对称式都可以用
,(m-1)(n-1)等神奇对称式都可以用![]() 表示.例如:
表示.例如:![]() .于是丽丽把
.于是丽丽把![]() 称为基本神奇对称式 .
称为基本神奇对称式 .
请根据以上材料解决下列问题:
(1)代数式①![]() , ②
, ②![]() , ③
, ③![]() , ④ xy + yz + zx中,属于神奇对称式的是__________(填序号);
, ④ xy + yz + zx中,属于神奇对称式的是__________(填序号);
(2)已知![]() .
.
① q=__________(用含m,n的代数式表示);
② 若![]() ,则神奇对称式
,则神奇对称式![]() =__________;
=__________;
③ 若![]() ,求神奇对称式
,求神奇对称式![]() 的最小值.
的最小值.
【答案】(1)①,④;(2)① q=mn.②![]() ;③-2.
;③-2.
【解析】
(1)根据题意新定义的神奇对称式任意交换两个字母的位置,式子的值不变来判断
(2)①由所学知识十字相乘法表示对应系数相等可求出
②把![]() 通分用mn与m+n的形式表示,然后转换成用p、q表示的代数式代入即可求出值
通分用mn与m+n的形式表示,然后转换成用p、q表示的代数式代入即可求出值
③把神奇对称式![]() 转换成用p、q表示的代数式,再根据求根公式求出范围
转换成用p、q表示的代数式,再根据求根公式求出范围
解:(1)①,④符合神奇对称式的定义,②③交换字母的位置,式子的值会变故不符合神奇对称式的定义。所以答案应为①,④
(2)①∵![]() ,
,
∴![]() .
.
故答案应为:q = mn .
②![]() =
=![]() =
=![]() = -
= -![]() 故答案应为-
故答案应为-![]()
③∵![]() ,
,
∴![]() .
.
![]()
= ![]()
=![]()
=![]() .
.
∵![]() ,
,
∴![]() .
.
即q=±p.
(i)当![]() 时,
时,
∴原式=![]() =
=![]() .
.
(ii)当![]() 时,
时,
∴原式=![]() =
=![]() .
.
综上,![]() 的最小值为-2.
的最小值为-2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】阅读材料:用配方法求最值.
已知x,y为非负实数,
∵x+y﹣![]()
∴x+y≥2![]() ,当且仅当“x=y”时,等号成立.
,当且仅当“x=y”时,等号成立.
示例:当x>0时,求y= x+![]() +4的最小值.
+4的最小值.
解:![]() +4=6
+4=6![]() ,当x=
,当x=![]() ,即x=1时,y的最小值为6.
,即x=1时,y的最小值为6.
(1)尝试:当x>0时,求y=![]() 的最小值.
的最小值.
(2)问题解决:随着人们生活水平的快速提高,小轿车已成为越来越多家庭的交通工具,假设某种小轿车的购车费用为10万元,每年应缴保险费等各类费用共计0.4万元,n年的保养、维护费用总和为![]() 万元.问这种小轿车使用多少年报废最合算(即:使用多少年的年平均费用最少,年平均费用=
万元.问这种小轿车使用多少年报废最合算(即:使用多少年的年平均费用最少,年平均费用=![]()
![]() )?最少年平均费用为多少万元?
)?最少年平均费用为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 、
、![]() 两地在一直线上,且相距
两地在一直线上,且相距![]() ,甲、乙两人同时从
,甲、乙两人同时从![]() 、
、![]() 出发,分别沿射线
出发,分别沿射线![]() 、
、![]() 行进,其中甲的速度为
行进,其中甲的速度为![]() ,设他们出发
,设他们出发![]() 时,甲、乙两人离
时,甲、乙两人离![]() 地的距离分别为
地的距离分别为![]() 、
、![]() ,
,![]() 与
与![]() 的部分函数图象如图所示:
的部分函数图象如图所示:

(1)分别写出![]() ,
,![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)在所给的平面直角坐标系中画出(1)中的函数图象,直接写出![]() 、
、![]() 的图象交点坐标并解释其实际意义.
的图象交点坐标并解释其实际意义.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆有50个房间供游客居住.当每个房间每天的定价为160元时,房间会全部住满;当每个房间每天定价每增加10元时,就会有一个房间空闲.如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用,房价定为多少时,宾馆利润最大?并求出一天的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①b2﹣4ac>0; ②abc>0; ③8a+c<0; ④9a+3b+c>0.其中,正确结论的个数( )
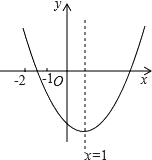
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
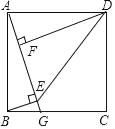
【题目】如图,正方形ABCD中,G为BC边上一点,BE⊥AG于E,DF⊥AG于F,连接DE.
(1)求证:△ABE≌△DAF;
(2)若AF=1,四边形ABED的面积为6,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某工程队在工地上利用互相垂直的两墙AE、AF,另两边用铁栅栏围成一个长方形场地ABCD,中间再用栅栏分割成两个长方形.铁栅栏总长180米,已知墙AE长90米,墙AF长60米.
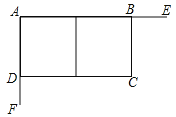
(1)设BC长为x米,长方形ABCD的面积为y,请写出y与x的函数关系,并写出x的取值范围;
(2)当BC的值为多少时,长方形ABCD的面积最大?
(3)若长方形ABCD的面积不能小于4000,请直接写出BC边长x(米)的取值范围 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE∥BA交AC于点E,DF∥CA交AB于点F,已知CD=3.
(1)求AD的长;
(2)求四边形AEDF的周长.(注意:本题中的计算过程和结果均保留根号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com