【题目】某宾馆有50个房间供游客居住.当每个房间每天的定价为160元时，房间会全部住满；当每个房间每天定价每增加10元时，就会有一个房间空闲.如果游客居住房间，宾馆需对每个房间每天支出20元的各种费用，房价定为多少时，宾馆利润最大？并求出一天的最大利润是多少？
科目：初中数学 来源： 题型：
【题目】某商店欲购进 A、B 两种商品，若购进 A 种商品 5 件和 B 种商品 4 件需 300 元；购进 A 种商品 6 件和 B 种商 品 8 件需 440 元.
（1）求 A、B 两种商品每件的进价分别为多少元？
（2）若该商店每销售 1 件 A 种商品可获利 8 元，每销售 1 件 B 种商品可获利 6 元，该商店准备购进 A、B 两种商 品共 50 件，且这两种商品全部售出后总获利超过 344 元，则至少购进多少件 A 商品？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在矩形ABCD中，AB=16cm，BC=6cm，动点P、Q分别以3cm/s，2cm/s的速度从点A，C同时出发，点Q从点C向点D移动.
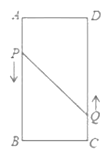
（1）设运动时间为
秒，则AP= cm，DQ= cm；
（2）若点P从点A移动到点B停止，点Q随点P的停止而停止移动，点P，Q分别从点A，C同时出发，问经过多长时间P，Q两点之间的距离是10cm？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】学以致用：问题1：怎样用长为
的铁丝围成一个面积最大的矩形？
小学时我们就知道结论：围成正方形时面积最大，即围成边长为
的正方形时面积最大为
．请用你所学的二次函数的知识解释原因．
思考验证：问题2：怎样用铁丝围一个面积为
且周长最小的矩形？
小明猜测：围成正方形时周长最小．
为了说明其中的道理，小明翻阅书籍，找到下面的结论：
在
、
均为正实数）中，若
为定值
，则
，只有当
时，
有最小值
．
思考验证：证明：
、均为正实数）
请完成小明的证明过程：
证明：对于任意正实数
、
解决问题：
（1）若
，则
（当且仅当
时取“
” 
；
（2）运用上述结论证明小明对问题2的猜测；
（3）填空：当
时，
的最小值为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下面材料：
丽丽这学期学习了轴对称的知识，知道了像角、等腰三角形、正方形、圆等图形都是轴对称图形.类比这一特性，丽丽发现像m+n，mnp，
等代数式，如果任意交换两个字母的位置，式子的值都不变.太神奇了！于是她把这样的式子命名为神奇对称式.
她还发现像
，(m-1)(n-1)等神奇对称式都可以用
表示.例如：
.于是丽丽把
称为基本神奇对称式 .
请根据以上材料解决下列问题：
（1）代数式①
， ②
， ③
， ④ xy + yz + zx中，属于神奇对称式的是__________（填序号）；
（2）已知
.
① q=__________（用含m，n的代数式表示）；
② 若
，则神奇对称式
=__________；
③ 若
，求神奇对称式
的最小值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某茶叶专卖店经销一种日照绿茶，每千克成本
元，据销售人员调查发现，每月的销售量
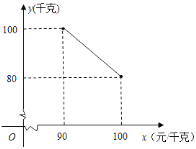
（千克）与销售单价
（元/千克）之间存在如图所示的变化规律．
求每月销售量与销售单价之间的函数关系式．
若某月该茶叶点销售这种绿茶获得利润
元，试求该月茶叶的销售单价为多少元．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，在Rt△ABC中，∠ACB=90°，AC=6cm，BC=8cm，点P从A出发沿AC向C点以1厘米/秒的速度匀速移动；点Q从C出发沿CB向B点以2厘米/秒的速度匀速移动．点P、Q分别从起点同时出发，移动到某一位置时所需时间为t秒．
（1）当t=2时，求线段PQ的长度；
（2）当t为何值时，△PCQ的面积等于5cm2？
（3）在P、Q运动过程中，在某一时刻，若将△PQC翻折，得到△EPQ，如图2，PE与AB能否垂直？若能，求出相应的t值；若不能，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
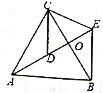
【题目】如图，△ACB和△DCE均为等腰三角形，点A、D、E在同一条直线上，BC和AE相交于点O，连接BE，若∠CAB=∠CBA=∠CDE=∠CED=50°。
（1）求证：AD=BE；
（2）求∠AEB。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
