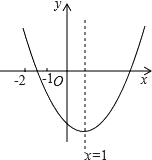
【题目】已知二次函数y＝ax2+bx+c（a≠0）的图象如图所示，有下列结论：①b2﹣4ac＞0； ②abc＞0； ③8a+c＜0； ④9a+3b+c＞0．其中，正确结论的个数（ ）
A. 1B. 2C. 3D. 4
【答案】B
【解析】
由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．
①由图知：抛物线与x轴有两个不同的交点，则△＝b2﹣4ac＞0，故①正确；
②抛物线开口向上，得：a＞0；对称轴为x
1，则b＝﹣2a，故b＜0；
抛物线交y轴于负半轴，得：c＜0；
所以abc＞0；故②正确；
③观察图象得当x＝﹣2时，y＞0，即4a﹣2b+c＞0．
∵b＝﹣2a，∴4a+4a+c＞0，即8a+c＞0，故③错误；
④根据抛物线的对称轴方程可知：（﹣1，0）关于对称轴的对称点是（3，0）；
当x＝﹣1时，y＜0，所以当x＝3时，也有y＜0，即9a+3b+c＜0；故④错误；
综上所述：正确的说法是：①②．
故选B．
阅读快车系列答案科目：初中数学 来源： 题型：
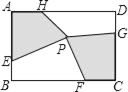
【题目】如图，矩形ABCD中，点E，F，G，H分别在边AB，BC，CD，DA上，点P在矩形ABCD内．若AB＝4cm，BC＝6cm，AE＝CG＝3cm，BF＝DH＝4cm，四边形AEPH的面积为5cm2，则四边形PFCG的面积为_______cm2．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，平行四边形ABCD的边OA在x轴上，将平行四边形沿对角线AC对折，AO的对应线段为AD，且点D，C，O在同一条直线上，AD与BC交于点E.
（1）求证：△ABC≌△CDA.
（2）若直线AB的函数表达式为
，求三角线ACE的面积.
查看答案和解析>>
科目：初中数学 来源： 题型：
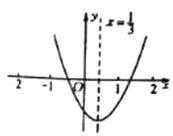
【题目】从如图所示的二次函数
的图象中，观察得出下面五条信息：①
；②
；③
；④
；⑤
.你认为其中正确信息的个数为（ ）
A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下面材料：
丽丽这学期学习了轴对称的知识，知道了像角、等腰三角形、正方形、圆等图形都是轴对称图形.类比这一特性，丽丽发现像m+n，mnp，
等代数式，如果任意交换两个字母的位置，式子的值都不变.太神奇了！于是她把这样的式子命名为神奇对称式.
她还发现像
，(m-1)(n-1)等神奇对称式都可以用
表示.例如：
.于是丽丽把
称为基本神奇对称式 .
请根据以上材料解决下列问题：
（1）代数式①
， ②
， ③
， ④ xy + yz + zx中，属于神奇对称式的是__________（填序号）；
（2）已知
.
① q=__________（用含m，n的代数式表示）；
② 若
，则神奇对称式
=__________；
③ 若
，求神奇对称式
的最小值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】将如图所示的牌面数字分别是1，2，3，4的四张扑克牌背面朝上，洗匀后放在桌面上．
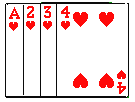
（1）从中随机抽出一张牌，牌面数字是偶数的概率是 ；
（2）从中随机抽出二张牌，两张牌牌面数字的和是5的概率是 ；
（3）先从中随机抽出一张牌，将牌面数字作为十位上的数字，然后将该牌放回并重新洗匀，再随机抽取一张，将牌面数字作为个位上的数字，请用画树状图或列表的方法求组成的两位数恰好是4的倍数的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，分别以直角
的斜边AB，直角边AC为边向外作等边
和等边
，F为AB的中点，DE与AB交于点G，EF与AC交于点H，
，
．给出如下结论：
①EF⊥AC； ②四边形ADFE为菱形； ③
； ④
；
其中正确结论的是( )
A. ①②③B. ②③④C. ①③④D. ①②④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】现代互联网技术的广泛应用，催生了快递行业的高速发展．阜阳市某家快递公司，2017年3月份与5月份完成投递的快递总件数分别为10万件和12.1万件．现假定该公司每月投递的快递总件数的增长率相同．
(1)求该快递公司投递快递总件数的月平均增长率？
(2) 如果平均每人每月最多可投递快递0.6万件，那么该公司现有的21名快递投递业务员能否完成2017年6月份的快递投递任务？如果不能，请问至少需要增加几名业务员？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
