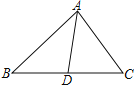
【题目】如图，
中，
，
是中线，
，则
_____
【答案】
【解析】
作CH⊥AD于H，延长AD到E使DE=AD=7，连接CE，作EF⊥AC于F，如图，先证明△ADB≌△EDC，得到EC=AB=10，再利用△AEF为等腰直角三角形，计算出AF=EF=
，则根据勾股定理可计算出CF=
，从而得到AC=
，接着利用△ACH为等腰直角三角形，得到AH=CH=6，然后利用勾股定理计算出CD，从而得到BC的长．
解：作CH⊥AD于H，延长AD到E使DE=AD=7，连接CE，作EF⊥AC于F，如图，
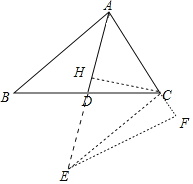
∵AD是中线，
∴BD=CD，
在△ADB和△EDC中
，
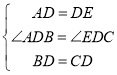∴△ADB≌△EDC（SAS），
∴EC=AB=10，
在RtAEF中，∵∠DAC=45°，AE=14，
∴AF=EF=
AE=，
在Rt△CEF中，
，
∴AC=AF-CF=，
在Rt△ACH中，∵∠HAC=45°，
∴AH=CH=AC=6，
∴DH=AD-AH=1，
在Rt△CDH中，CD=
∴BC=2CD=，
故答案为：．
科目：初中数学 来源： 题型：
【题目】哈市在迎接文明城市检查期间，提出了核心价值观“包容、尚德、守法、诚信、卓越”．为了了解学生对城市核心 价值观中哪一项内容最感兴趣，对某所中学的学生抽查：随机抽取了部分学生进行调查，并将调查结果绘成如图 统计图．请你结合图中信息解答下列问题：
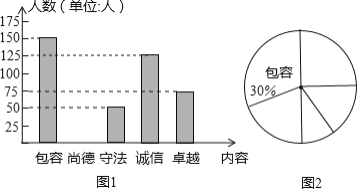
（1）该校共调查了多少名学生，并补全条形统计图；
（2）如果全校有学生 2500 人，请你估计全校中 对“诚信”最感兴趣的学生有多少名？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数y＝ax2+bx+c（a≠0）的图象如图所示，有下列结论：①b2﹣4ac＞0； ②abc＞0； ③8a+c＜0； ④9a+3b+c＞0．其中，正确结论的个数（ ）
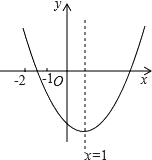
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某宾馆拥有客房100间，经营中发现：每天入住的客房数y(间)与房价x(元)(180≤x≤300)满足一次函数关系，部分对应值如下表：
x(元) | 180 | 260 | 280 | 300 |
y(间) | 100 | 60 | 50 | 40 |
(1)求y与x之间的函数表达式；
(2)已知每间入住的客房，宾馆每日需支出各种费用100元；每间空置的客房，宾馆每日需支出各种费用60元．当房价为多少元时，宾馆当日利润最大？求出最大利润．(宾馆当日利润=当日房费收入-当日支出)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，某工程队在工地上利用互相垂直的两墙AE、AF，另两边用铁栅栏围成一个长方形场地ABCD，中间再用栅栏分割成两个长方形．铁栅栏总长180米，已知墙AE长90米，墙AF长60米．
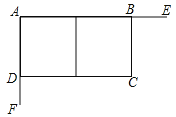
（1）设BC长为x米，长方形ABCD的面积为y，请写出y与x的函数关系，并写出x的取值范围；
（2）当BC的值为多少时，长方形ABCD的面积最大？
（3）若长方形ABCD的面积不能小于4000，请直接写出BC边长x（米）的取值范围 .
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC的顶点坐标分别为A(0，1)、B(3，3)、C(1，3).
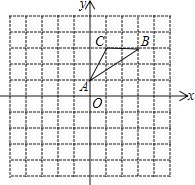
(1) 画出△ABC关于点O的中心对称图形△A1B1C1
(2) 画出△ABC绕原点O逆时针旋转90°的△A2B2C2，直接写出点C2的坐标为______.
(3) 若△ABC内一点P(m，n)绕原点O逆时针旋转90°的对应点为Q，则Q的坐标为______.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知关于x的方程 x2﹣（2k+1）x+4（k﹣
）＝0．若等腰三角形ABC的一边长a＝4，另两边边长b、c恰好是这个方程的两个实数根，则△ABC的周长为_____．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
