
【题目】已知关于x的方程 x2﹣(2k+1)x+4(k﹣![]() )=0.若等腰三角形ABC的一边长a=4,另两边边长b、c恰好是这个方程的两个实数根,则△ABC的周长为_____.
)=0.若等腰三角形ABC的一边长a=4,另两边边长b、c恰好是这个方程的两个实数根,则△ABC的周长为_____.
【答案】10
【解析】
分a为腰长以及底边长两种情况考虑.①等a为腰长时,将x=4代入原方程可求出k值,将k值代入原方程解方程可得出底边长,再利用三角形的三边关系验证后可得出结论;②当a为底边长时,根据根的判别式△=0即可求出k值,将k值代入原方程解方程可得出腰长,再利用三角形的三边关系验证后即可得出结论.综上即可得出结论.
解:①当a为腰长时,将x=4代入x2﹣(2k+1)x+4(k﹣![]() )=0中得:10﹣4k=0,
)=0中得:10﹣4k=0,
解得:k=![]() ,
,
∴原方程为x2﹣6x+8=0,
解得:x1=4,x2=2,
∵4,4,2满足任意两边之和大于第三边,
∴C=4+4+2=10;
②当a为底边长时,方程 x2﹣(2k+1)x+4(k﹣![]() )=0有两个相等的实数根,
)=0有两个相等的实数根,
∴△=[﹣(2k+1)]2﹣4×1×4(k﹣![]() )=4k2﹣12k+9=0,
)=4k2﹣12k+9=0,
解得:k=![]() .
.
当k=![]() 时,原方程为x2﹣4x+4=0,
时,原方程为x2﹣4x+4=0,
解得:x=2,
∵2,2,4不满足任意两边之和大于第三边,
∴a为底边长不符合题意.
综上可知:△ABC的周长为10.
故答案为:10.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的边OA在x轴上,将平行四边形沿对角线AC对折,AO的对应线段为AD,且点D,C,O在同一条直线上,AD与BC交于点E.

(1)求证:△ABC≌△CDA.
(2)若直线AB的函数表达式为![]() ,求三角线ACE的面积.
,求三角线ACE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以直角![]() 的斜边AB,直角边AC为边向
的斜边AB,直角边AC为边向![]() 外作等边
外作等边![]() 和等边
和等边![]() ,F为AB的中点,DE与AB交于点G,EF与AC交于点H,
,F为AB的中点,DE与AB交于点G,EF与AC交于点H,![]() ,
,![]() .给出如下结论:
.给出如下结论:
①EF⊥AC; ②四边形ADFE为菱形; ③![]() ; ④
; ④![]() ;
;
其中正确结论的是( )

A. ①②③B. ②③④C. ①③④D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=-![]() x+4与x轴、y轴分别交于点A,点B、点D在y轴的负半轴上,若将△OAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处。
x+4与x轴、y轴分别交于点A,点B、点D在y轴的负半轴上,若将△OAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处。
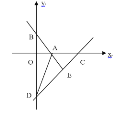
(1)求AB的长。
(2)求点C和点D的坐标。
(3)y轴上是否存在一点P,S△PAB= ![]() S△OCD?
S△OCD?
查看答案和解析>>
科目:初中数学 来源: 题型:
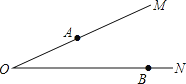
【题目】如图,∠MON=20°,A、B分别为射线OM、ON上两定点,且OA=2,OB=4,点P、Q分别为射线OM、ON两动点,当P、Q运动时,线段AQ+PQ+PB的最小值是( )
A.3B.![]() C.2D.
C.2D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某新型高科技商品,每件的售价比进价多6元,5件的进价相当于4件的售价,每天可售出200件,经市场调查发现,如果每件商品涨价1元,每天就会少卖5件.
(1)该商品的售价和进价分别是多少元?
(2)设每天的销售利润为w元,每件商品涨价x元,则当售价为多少元时,该商品每天的销售利润最大,最大利润为多少元?
(3)为增加销售利润,营销部推出了以下两种销售方案:方案一:每件商品涨价不超过8元;方案二:每件商品的利润至少为24元,请比较哪种方案的销售利润更高,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.阜阳市某家快递公司,2017年3月份与5月份完成投递的快递总件数分别为10万件和12.1万件.现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递快递总件数的月平均增长率?
(2) 如果平均每人每月最多可投递快递0.6万件,那么该公司现有的21名快递投递业务员能否完成2017年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com