
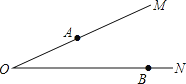
【题目】如图,∠MON=20°,A、B分别为射线OM、ON上两定点,且OA=2,OB=4,点P、Q分别为射线OM、ON两动点,当P、Q运动时,线段AQ+PQ+PB的最小值是( )
A.3B.![]() C.2D.
C.2D.![]()
【答案】D
【解析】
首先作A关于ON的对称点A′,点B关于OM的对称点B′,连接A′B′,交于OM,ON分别为P,Q,连接OA′,OB′,可求得AQ+PQ+PB=A′Q+PQ+PB′=A′B′,∠A′OB′=60°,然后由特殊角的三角函数值,判定∠OA′B′=90°,再利用勾股定理求得答案.
作A关于ON的对称点A′,点B关于OM的对称点B′,连接A′B′,交于OM,ON分别为P,Q,连接OA′,OB′,
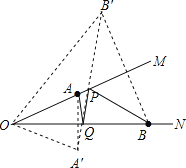
则PB′=PB,AQ=A′Q,OA′=OA=2,OB′=OB=4,∠MOB′=∠NOA′=∠MON=20°,
∴AQ+PQ+PB=A′Q+PQ+PB′=A′B′,∠A′OB′=60°,
∵![]() ,
,
∴∠OA′B′=90°,
∴A′B′=![]() ,
,
∴线段AQ+PQ+PB的最小值是:![]() .
.
故答案为D.


科目:初中数学 来源: 题型:
【题目】某宾馆拥有客房100间,经营中发现:每天入住的客房数y(间)与房价x(元)(180≤x≤300)满足一次函数关系,部分对应值如下表:
x(元) | 180 | 260 | 280 | 300 |
y(间) | 100 | 60 | 50 | 40 |
(1)求y与x之间的函数表达式;
(2)已知每间入住的客房,宾馆每日需支出各种费用100元;每间空置的客房,宾馆每日需支出各种费用60元.当房价为多少元时,宾馆当日利润最大?求出最大利润.(宾馆当日利润=当日房费收入-当日支出)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的顶点坐标分别为A(0,1)、B(3,3)、C(1,3).
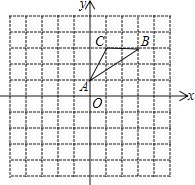
(1) 画出△ABC关于点O的中心对称图形△A1B1C1
(2) 画出△ABC绕原点O逆时针旋转90°的△A2B2C2,直接写出点C2的坐标为______.
(3) 若△ABC内一点P(m,n)绕原点O逆时针旋转90°的对应点为Q,则Q的坐标为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程 x2﹣(2k+1)x+4(k﹣![]() )=0.若等腰三角形ABC的一边长a=4,另两边边长b、c恰好是这个方程的两个实数根,则△ABC的周长为_____.
)=0.若等腰三角形ABC的一边长a=4,另两边边长b、c恰好是这个方程的两个实数根,则△ABC的周长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c开口向上,与x轴交于点A、B,与y轴交于点C

(1) 如图1,若A (1,0)、C (0,3)且对称轴为直线x=2,求抛物线的解析式
(2) 在(1)的条件下,如图2,作点C关于抛物线对称轴的对称点D,连接AD、BD,在抛物线上是否存在点P,使∠PAD=∠ADB,若存在,求出点P的坐标,若不存在,请说明理由
(3) 若直线l:y=mx+n与抛物线有两个交点M、N(M在N的左边),Q为抛物线上一点(不与M、N重合),过点Q作QH平行于y轴交直线l于点H,求![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′.若∠A=40°,∠B′=110°,则∠BCA′的度数是( )

A.90°B.80°C.50°D.30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 与一次函数
与一次函数![]() ,令W=
,令W=![]() .
.
(1)若![]() 、
、![]() 的函数图像交于x轴上的同一点.
的函数图像交于x轴上的同一点.
①求![]() 的值;
的值;
②当![]() 为何值时,W的值最小,试求出该最小值;
为何值时,W的值最小,试求出该最小值;
(2)当![]() 时,W随x的增大而减小.
时,W随x的增大而减小.
①求![]() 的取值范围;
的取值范围;
②求证: ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com