练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

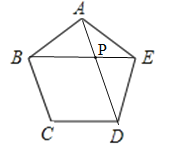
    【题目】如图，在正五边形ABCDE中每个内角是108°，请使用无刻度的直尺画出一个以B，C，D，P为顶点的菱形并说明理由.

    【答案】连结AD，BE相交于点P，则四边形BCDP为所求作的菱形．理由见解析．

    【解析】

    连结AD，BE相交于点P，则四边形BCDP为菱形．首先由正五边形的性质可得AB=BC=CD，BC∥PD，CD∥BP，得到四边形BCDP是平行四边形，再根据有一组邻边相等的平行四边形是菱形即可证．

    连结AD，BE相交于点P，则四边形BCDP为所求作的菱形．

    理由：∵正五边形ABCDE的内角108°，∴∠C=∠ABC=∠BAE=108°，AB=BC=CD=AE，∴∠ABE=36°，∴∠EBC=∠ABC-∠ABE=72°，∴∠EBC+∠C=180°，∴BC∥PD．

    同理得：CD∥BP，∴四边形BCDP是平行四边形．

    又∵BC=CD，∴四边形BCDP是菱形．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，直线L上有三个正方形a，b，c，若a，c的面积分别为1和9，则b的面积为（ ）

    A．8 B．9 C．10 D．11

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数y＝ax2+bx+c（a≠0）的图象如图所示，并且关于x的一元二次方程ax2+bx+c﹣m＝0有两个不相等的实数根，下列结论：①b2﹣4ac＜0；②abc＞0；③a﹣b+c＜0；④m＞﹣2，其中，正确的个数有（　　）

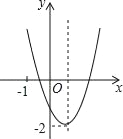
    A. 1 B. 2 C. 3 D. 4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，⊙O的直径AB为8cm,∠B=300, ∠ACB的平分线交⊙O于D，连接AD．

    （1）求BC的长；

    （2）求∠CAD的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，平行四边形ABCD的边OA在x轴上，将平行四边形沿对角线AC对折，AO的对应线段为AD，且点D，C，O在同一条直线上，AD与BC交于点E.

    （1）求证：△ABC≌△CDA.

    （2）若直线AB的函数表达式为，求三角线ACE的面积.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在“爱满扬州”慈善一日捐活动中，学校团总支为了了解本校学生的捐款情况，随机抽取了50名学生的捐款数进行了统计，并绘制成统计图．

    （1）这50名同学捐款的众数为 元，中位数为 元；

    （2）求这50名同学捐款的平均数；

    （3）该校共有600名学生参与捐款，请估计该校学生的捐款总数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】从如图所示的二次函数的图象中，观察得出下面五条信息：①；②；③；④；⑤.你认为其中正确信息的个数为（ ）

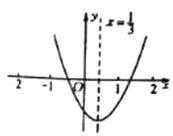
    A. 2个B. 3个C. 4个D. 5个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】将如图所示的牌面数字分别是1，2，3，4的四张扑克牌背面朝上，洗匀后放在桌面上．

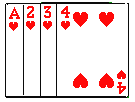
    （1）从中随机抽出一张牌，牌面数字是偶数的概率是 ；

    （2）从中随机抽出二张牌，两张牌牌面数字的和是5的概率是 ；

    （3）先从中随机抽出一张牌，将牌面数字作为十位上的数字，然后将该牌放回并重新洗匀，再随机抽取一张，将牌面数字作为个位上的数字，请用画树状图或列表的方法求组成的两位数恰好是4的倍数的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，∠MON=20°，A、B分别为射线OM、ON上两定点，且OA=2，OB=4，点P、Q分别为射线OM、ON两动点，当P、Q运动时，线段AQ+PQ+PB的最小值是（　　）

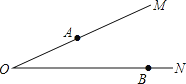
    A.3B.C.2D.

    查看答案和解析>>

    同步练习册答案