
【题目】如图,在平面直角坐标系中,直线y=-![]() x+4与x轴、y轴分别交于点A,点B、点D在y轴的负半轴上,若将△OAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处。
x+4与x轴、y轴分别交于点A,点B、点D在y轴的负半轴上,若将△OAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处。
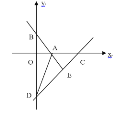
(1)求AB的长。
(2)求点C和点D的坐标。
(3)y轴上是否存在一点P,S△PAB= ![]() S△OCD?
S△OCD?
【答案】(1)AB=5;(2)C(8,0),D(0,-6);(3)P1(0,12),P2(0,-4),见解析.
【解析】
(1)先求得点A和点B的坐标,则可得到OA、OB的长,然后依据勾股定理可求得AB的长,
(2)依据翻折的性质可得到AC的长,于是可求得OC的长,从而可得到点C的坐标;设OD=x,则CD=DB=x+4.,Rt△OCD中,依据勾股定理可求得x的值,从而可得到点D(0,-6).
(3)先求得S△PAB的值,然后依据三角形的面积公式可求得BP的长,从而可得到点P的坐标.
(1)令x=0得:y=4,
∴B(0,4).
∴OB=4
令y=0得:0=![]() x+4,解得:x=3,
x+4,解得:x=3,
∴A(3,0).
∴OA=3.
在Rt△OAB中,AB=![]() =5.
=5.
(2) ∵AB=5,
∴OC=OA+AC=3+5=8,
∴C(8,0).
设OD=x,则CD=DB=x+4.
在Rt△OCD中,DC2=OD2+OC2,即(x+4)2=x2+82,解得:x=6,
∴D(0,6).
(3)∵S△PAB=![]() S△OCD,
S△OCD,
∴S△PAB=![]() ×
×![]() ×6×8=12.
×6×8=12.
∵点P在y轴上,S△PAB=12,
∴![]() BPOA=12,即
BPOA=12,即![]() ×3BP=12,解得:BP=8,
×3BP=12,解得:BP=8,
∴P1(0,12),P2(0,-4),.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】阅读材料:用配方法求最值.
已知x,y为非负实数,
∵x+y﹣![]()
∴x+y≥2![]() ,当且仅当“x=y”时,等号成立.
,当且仅当“x=y”时,等号成立.
示例:当x>0时,求y= x+![]() +4的最小值.
+4的最小值.
解:![]() +4=6
+4=6![]() ,当x=
,当x=![]() ,即x=1时,y的最小值为6.
,即x=1时,y的最小值为6.
(1)尝试:当x>0时,求y=![]() 的最小值.
的最小值.
(2)问题解决:随着人们生活水平的快速提高,小轿车已成为越来越多家庭的交通工具,假设某种小轿车的购车费用为10万元,每年应缴保险费等各类费用共计0.4万元,n年的保养、维护费用总和为![]() 万元.问这种小轿车使用多少年报废最合算(即:使用多少年的年平均费用最少,年平均费用=
万元.问这种小轿车使用多少年报废最合算(即:使用多少年的年平均费用最少,年平均费用=![]()
![]() )?最少年平均费用为多少万元?
)?最少年平均费用为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
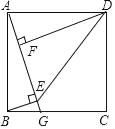
【题目】如图,正方形ABCD中,G为BC边上一点,BE⊥AG于E,DF⊥AG于F,连接DE.
(1)求证:△ABE≌△DAF;
(2)若AF=1,四边形ABED的面积为6,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某工程队在工地上利用互相垂直的两墙AE、AF,另两边用铁栅栏围成一个长方形场地ABCD,中间再用栅栏分割成两个长方形.铁栅栏总长180米,已知墙AE长90米,墙AF长60米.
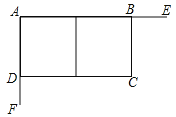
(1)设BC长为x米,长方形ABCD的面积为y,请写出y与x的函数关系,并写出x的取值范围;
(2)当BC的值为多少时,长方形ABCD的面积最大?
(3)若长方形ABCD的面积不能小于4000,请直接写出BC边长x(米)的取值范围 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,AB=BC,∠B=∠C=90°,P是BC边上一点,AP⊥PD,E是AB边上一点,∠BPE=∠BAP.
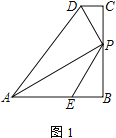
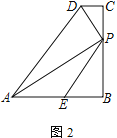
(1) 如图1,若AE=PE,直接写出![]() =______;
=______;
(2) 如图2,求证:AP=PD+PE;
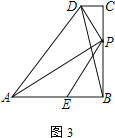
(3) 如图3,当AE=BP时,连BD,则![]() =______,并说明理由.
=______,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程 x2﹣(2k+1)x+4(k﹣![]() )=0.若等腰三角形ABC的一边长a=4,另两边边长b、c恰好是这个方程的两个实数根,则△ABC的周长为_____.
)=0.若等腰三角形ABC的一边长a=4,另两边边长b、c恰好是这个方程的两个实数根,则△ABC的周长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE∥BA交AC于点E,DF∥CA交AB于点F,已知CD=3.
(1)求AD的长;
(2)求四边形AEDF的周长.(注意:本题中的计算过程和结果均保留根号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com