
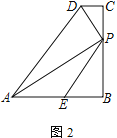
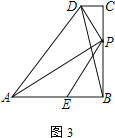
【题目】四边形ABCD中,AB=BC,∠B=∠C=90°,P是BC边上一点,AP⊥PD,E是AB边上一点,∠BPE=∠BAP.
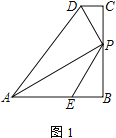
(1) 如图1,若AE=PE,直接写出![]() =______;
=______;
(2) 如图2,求证:AP=PD+PE;
(3) 如图3,当AE=BP时,连BD,则![]() =______,并说明理由.
=______,并说明理由.
【答案】(1)![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]() .
.
【解析】
(1)首先证明∠PAB=30°,设PB=a,可得AB=BC![]() a,求出PC即可解决问题;
a,求出PC即可解决问题;
(2)如图2中,延长DP交AB的延长线于M,作MN⊥DC交DC的延长线于N.首先证明PE=PM,再证明△ABP≌△MND(ASA)即可解决问题;
(3)如图3,延长DP交AB的延长线于M,作MN⊥DC交DC的延长线于N.首先证明DN=PB=AE,EB=BM=CN,设AE=PB=DN=x,EB=BM=CN=y,求出PE,BD即可解决问题.
(1)如图1.

∵AE=PE,∴∠EAP=∠EPA.
∵∠EPB=∠PAE,∴∠EPB=∠PAE=∠EPA.
∵∠B=90°,∴∠PAB+∠APB=90°,∴3∠PAE=90°,∴∠PAE=30°.
设PB=a,则AB=BC![]() a,∴PC=BC﹣PB
a,∴PC=BC﹣PB![]() a﹣a,∴
a﹣a,∴![]() 1.
1.
故答案为:![]() .
.
(2)如图2,延长DP交AB的延长线于M,作MN⊥DC交DC的延长线于N.
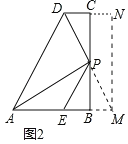
∵AP⊥DM,∴∠APM=∠PBM=90°.
∵∠PAE+∠APB=90°,∠APB+∠BPM=90°,∴∠PAE=∠BPM.
∵∠EPB=∠PAE,∴∠EPB=∠BPM.
∵∠EPB+∠PEB=90°,∠BPM+∠PMB=90°,∴∠PEB=∠PMB,∴PE=PM.
∵∠CBM=∠BCN=∠N=90°,∴四边形BCNM是矩形,∴BC=MN=AB,BC∥MN,∴∠DMN=∠BPM=∠PAB.
∵∠ABP=∠N=90°,∴△ABP≌△MND(ASA),∴PA=DM.
∵DM=DP+PM=DP+PE,∴PA=DP+PE.
(3)如图3,延长DP交AB的延长线于M,作MN⊥DC交DC的延长线于N.
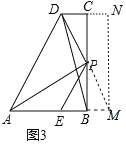
由(2)可知:PE=PM,△ABP≌△MND,四边形BCNM是矩形,∴PB=DN,设PB=DN=x,∴AE=PB=DN=x.
∵PE=PM,PB⊥EM,∴EB=BM.
∵BM=CN,∴BE=BM=CN,设BE=BM=CN=y,则CD=x﹣y,BC=AB=x+y.
在Rt△PBE中,PE![]() .在Rt△DCB中,BD
.在Rt△DCB中,BD![]() ,∴
,∴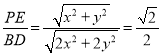 .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】某商店欲购进 A、B 两种商品,若购进 A 种商品 5 件和 B 种商品 4 件需 300 元;购进 A 种商品 6 件和 B 种商 品 8 件需 440 元.
(1)求 A、B 两种商品每件的进价分别为多少元?
(2)若该商店每销售 1 件 A 种商品可获利 8 元,每销售 1 件 B 种商品可获利 6 元,该商店准备购进 A、B 两种商 品共 50 件,且这两种商品全部售出后总获利超过 344 元,则至少购进多少件 A 商品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某茶叶专卖店经销一种日照绿茶,每千克成本![]() 元,据销售人员调查发现,每月的销售量
元,据销售人员调查发现,每月的销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元/千克)之间存在如图所示的变化规律.
(元/千克)之间存在如图所示的变化规律.
![]() 求每月销售量
求每月销售量![]() 与销售单价
与销售单价![]() 之间的函数关系式.
之间的函数关系式.
![]() 若某月该茶叶点销售这种绿茶获得利润
若某月该茶叶点销售这种绿茶获得利润![]() 元,试求该月茶叶的销售单价
元,试求该月茶叶的销售单价![]() 为多少元.
为多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,点P从A出发沿AC向C点以1厘米/秒的速度匀速移动;点Q从C出发沿CB向B点以2厘米/秒的速度匀速移动.点P、Q分别从起点同时出发,移动到某一位置时所需时间为t秒.

(1)当t=2时,求线段PQ的长度;
(2)当t为何值时,△PCQ的面积等于5cm2?
(3)在P、Q运动过程中,在某一时刻,若将△PQC翻折,得到△EPQ,如图2,PE与AB能否垂直?若能,求出相应的t值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=-![]() x+4与x轴、y轴分别交于点A,点B、点D在y轴的负半轴上,若将△OAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处。
x+4与x轴、y轴分别交于点A,点B、点D在y轴的负半轴上,若将△OAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处。
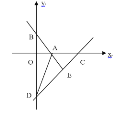
(1)求AB的长。
(2)求点C和点D的坐标。
(3)y轴上是否存在一点P,S△PAB= ![]() S△OCD?
S△OCD?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学课外活动小组准备围建一个矩形生物苗圃园,其中一边靠墙,另外三边用长为30米的篱笆围成,已知墙长为18米.设这个苗圃园垂直于墙的一边的长为x米
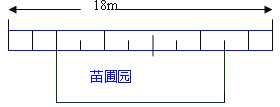
(1)用含x的代数式表示平行于墙的一边的长为____米,.x的取值范围为____
(2)这个苗圃园的面积为88平方米时,求x的值
查看答案和解析>>
科目:初中数学 来源: 题型:
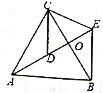
【题目】如图,△ACB和△DCE均为等腰三角形,点A、D、E在同一条直线上,BC和AE相交于点O,连接BE,若∠CAB=∠CBA=∠CDE=∠CED=50°。
(1)求证:AD=BE;
(2)求∠AEB。
查看答案和解析>>
科目:初中数学 来源: 题型:
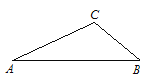
【题目】已知△ABC中,∠A=25°,∠B=40°.
(1)求作:⊙O,使⊙O经过A、C两点,且圆心落在AB边上;
(要求:尺规作图,保留作图痕迹,不写作法.)
(2)求证:BC是(1)中所作⊙O的切线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com