
����Ŀ���Ķ����ϣ����䷽������ֵ��
��֪x��yΪ�Ǹ�ʵ����
��x+y��![]()
��x+y��2![]() �����ҽ�����x=y��ʱ���Ⱥų�����
�����ҽ�����x=y��ʱ���Ⱥų�����
ʾ������x��0ʱ����y= x+![]() +4����Сֵ��
+4����Сֵ��
�⣺![]() +4=6
+4=6![]() ����x=
����x=![]() ����x=1ʱ��y����СֵΪ6��
����x=1ʱ��y����СֵΪ6��
��1�����ԣ���x��0ʱ����y=![]() ����Сֵ��
����Сֵ��
��2����������������������ˮƽ�Ŀ�����ߣ�С�γ��ѳ�ΪԽ��Խ���ͥ�Ľ�ͨ���ߣ�����ij��С�γ��Ĺ�������Ϊ10��Ԫ��ÿ��Ӧ�ɱ��շѵȸ�����ù���0.4��Ԫ��n��ı�����ά�������ܺ�Ϊ![]() ��Ԫ��������С�γ�ʹ�ö����걨������㣨����ʹ�ö��������ƽ���������٣���ƽ������=
��Ԫ��������С�γ�ʹ�ö����걨������㣨����ʹ�ö��������ƽ���������٣���ƽ������=![]()
![]() ����������ƽ������Ϊ������Ԫ��
����������ƽ������Ϊ������Ԫ��
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ������������������6�������Σ��١�ABC���ڡ�BCD���ۡ�BDE���ܡ�BFG���ݡ�FGH���ޡ�EFK.���Т�������������Ƶ���( )

A. �ڢۢ� B. �ۢܢ� C. �ܢݢ� D. �ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
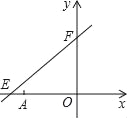
����Ŀ����ͼ��ֱ��y=![]() x+6��x�ᡢy��ֱ��ཻ�ڵ�E��F����A������Ϊ����6��0����P��x��y����ֱ��y=
x+6��x�ᡢy��ֱ��ཻ�ڵ�E��F����A������Ϊ����6��0����P��x��y����ֱ��y=![]() x+6��һ�����㣮
x+6��һ�����㣮
��1���ڵ�P�˶������У���д����OPA�����s��x�ĺ�����ϵʽ��
��2����P�˶���ʲôλ�ã���OPA�����Ϊ![]() �������ʱ��P�����ꣻ
�������ʱ��P�����ꣻ
��3����P��EF�Ĵ��߷ֱ�x�ᡢy����C��D���Ƿ���������ĵ�P��ʹ��COD�ա�FOE�������ڣ�ֱ��д����ʱ��P�����꣨��Ҫ��д�����̣����������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������x�Ķ��κ���![]() ��ͼ����x�ύ�ڵ�A(1��0)�͵�B����y�ύ�ڵ�C(0��3)�������ߵĶԳ�����x�ύ�ڵ�D.
��ͼ����x�ύ�ڵ�A(1��0)�͵�B����y�ύ�ڵ�C(0��3)�������ߵĶԳ�����x�ύ�ڵ�D.
(1)����κ����ı���ʽ��
(2)��y�����Ƿ����һ��P��ʹ��PBCΪ����������.�����ڣ��������P�����ꣻ
(3)��һ����M�ӵ�A��������ÿ��1����λ���ٶ���AB�����B�˶�����һ����N�ӵ�D���Mͬʱ��������ÿ��2����λ���ٶ��������ߵĶԳ������˶�������M�� ���Bʱ����M��Nͬʱֹͣ�˶����ʵ�M��N�˶����δ�ʱ����MNB�����������������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵������� A��B ������Ʒ�������� A ����Ʒ 5 ���� B ����Ʒ 4 ���� 300 Ԫ������ A ����Ʒ 6 ���� B ���� Ʒ 8 ���� 440 Ԫ.
��1���� A��B ������Ʒÿ���Ľ��۷ֱ�Ϊ����Ԫ��
��2�������̵�ÿ���� 1 �� A ����Ʒ�ɻ��� 8 Ԫ��ÿ���� 1 �� B ����Ʒ�ɻ��� 6 Ԫ�����̵������� A��B ������ Ʒ�� 50 ��������������Ʒȫ���۳����ܻ������� 344 Ԫ�������ٹ������ټ� A ��Ʒ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ���ı���ABCD�ı�OA��x���ϣ���ƽ���ı����ضԽ���AC���ۣ�AO�Ķ�Ӧ�߶�ΪAD���ҵ�D��C��O��ͬһ��ֱ���ϣ�AD��BC���ڵ�E.

��1����֤����ABC�ա�CDA.
��2����ֱ��AB�ĺ�������ʽΪ![]() ����������ACE�����.
����������ACE�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AB=16cm��BC=6cm������P��Q�ֱ���3cm/s��2cm/s���ٶȴӵ�A��Cͬʱ��������Q�ӵ�C���D�ƶ�.
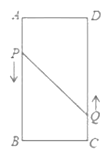
��1�����˶�ʱ��Ϊ![]() �룬��AP= cm��DQ= cm��
�룬��AP= cm��DQ= cm��
��2������P�ӵ�A�ƶ�����Bֹͣ����Q���P��ֹͣ��ֹͣ�ƶ�����P��Q�ֱ�ӵ�A��Cͬʱ�������ʾ����ʱ��P��Q����֮��ľ�����10cm��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������ϣ�
������ѧ��ѧϰ����ԳƵ�֪ʶ��֪������ǡ����������Ρ������Ρ�Բ��ͼ�ζ�����Գ�ͼ��.�����һ���ԣ�����������m+n��mnp��![]() �ȴ���ʽ��������⽻��������ĸ��λ�ã�ʽ�ӵ�ֵ������.̫�����ˣ���������������ʽ������Ϊ����Գ�ʽ.
�ȴ���ʽ��������⽻��������ĸ��λ�ã�ʽ�ӵ�ֵ������.̫�����ˣ���������������ʽ������Ϊ����Գ�ʽ.
����������![]() ��(m-1)(n-1)������Գ�ʽ��������
��(m-1)(n-1)������Գ�ʽ��������![]() ��ʾ.���磺
��ʾ.���磺![]() .����������
.����������![]() ��Ϊ��������Գ�ʽ .
��Ϊ��������Գ�ʽ .
��������ϲ��Ͻ���������⣺
��1������ʽ��![]() �� ��
�� ��![]() �� ��
�� ��![]() �� �� xy + yz + zx�У���������Գ�ʽ����__________������ţ���
�� �� xy + yz + zx�У���������Գ�ʽ����__________������ţ���
��2����֪![]() .
.
�� q=__________���ú�m��n�Ĵ���ʽ��ʾ����
�� ��![]() ��������Գ�ʽ
��������Գ�ʽ![]() =__________��
=__________��
�� ��![]() ��������Գ�ʽ
��������Գ�ʽ![]() ����Сֵ.
����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y=��![]() x+4��x�ᡢy��ֱ��ڵ�A����B����D��y��ĸ������ϣ�������OAB��ֱ��AD�۵�����Bǡ������x���������ϵĵ�C����
x+4��x�ᡢy��ֱ��ڵ�A����B����D��y��ĸ������ϣ�������OAB��ֱ��AD�۵�����Bǡ������x���������ϵĵ�C����
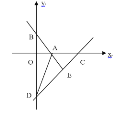
��1����AB�ij���
��2�����C�͵�D�����ꡣ
��3��y�����Ƿ����һ��P��S��PAB= ![]() S��OCD?
S��OCD?
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com