
分析 首先根据分式混合运算的运算方法,把原式进行化简,然后把x=$\sqrt{2}$+1代入化简后的算式,求出算式x+1-$\frac{{x}^{2}}{x-1}$的值是多少即可.
解答 解:x+1-$\frac{{x}^{2}}{x-1}$
=$\frac{(x+1)(x-1)}{x-1}-\frac{{x}^{2}}{x-1}$
=$\frac{{x}^{2}-1}{x-1}-\frac{{x}^{2}}{x-1}$
=$-\frac{1}{x-1}$,
当x=$\sqrt{2}$+1时,
$-\frac{1}{x-1}$=-$\frac{1}{\sqrt{2}+1-1}=-\frac{1}{\sqrt{2}}=-\frac{\sqrt{2}}{2}$.
点评 此题主要考查了分式的化简求值问题,注意化简时不能跨度太大,而缺少必要的步骤,解答此题的关键是要明确:代入求值时,有直接代入法,整体代入法等常用方法.解题时可根据题目的具体条件选择合适的方法.当未知数的值没有明确给出时,所选取的未知数的值必须使原式中的各分式都有意义,且除数不能为0.


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:解答题
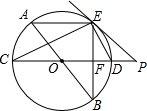 如图,AB、CD为⊙O的直径,弦AE∥CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使∠PED=∠C.
如图,AB、CD为⊙O的直径,弦AE∥CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使∠PED=∠C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
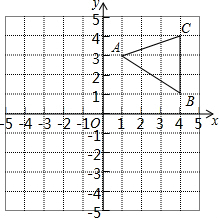 如图,已知△ABC三个顶点坐标分别是A(1,3),B(4,1),C(4,4).
如图,已知△ABC三个顶点坐标分别是A(1,3),B(4,1),C(4,4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
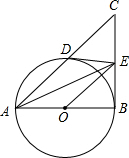 如图,△ABC中∠ABC=90°,以AB为直径作⊙O,与AC交于点D,点E为DC中点,连DE
如图,△ABC中∠ABC=90°,以AB为直径作⊙O,与AC交于点D,点E为DC中点,连DE查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | C或E | B. | B或D | C. | A或C | D. | B或F |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com