
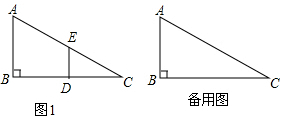
 ��ͼ1����Rt��ABC�У���B=90�㣬BC=2AB=8����D��E�ֱ��DZ�BC��AC���е㣬����DE������EDC�Ƶ�C��˳ʱ�뷽����ת������ת��Ϊ����
��ͼ1����Rt��ABC�У���B=90�㣬BC=2AB=8����D��E�ֱ��DZ�BC��AC���е㣬����DE������EDC�Ƶ�C��˳ʱ�뷽����ת������ת��Ϊ�������� ��1���ٵ���=0��ʱ����Rt��ABC�У��ɹ��ɶ��������AC��ֵ�Ƕ��٣�Ȼ����ݵ�D��E�ֱ��DZ�BC��AC���е㣬�ֱ����AE��BD�Ĵ�С�����������$\frac{AE}{BD}$ֵ�Ƕ��٣�
�ڦ�=180��ʱ���ɵ�AB��DE��Ȼ�����$\frac{AC}{AE}$=$\frac{BC}{BD}$�����$\frac{AE}{BD}$��ֵ���ɣ�
�������жϳ���ECA=��DCB���ٸ���$\frac{EC}{DC}$=$\frac{AC}{BC}$=$\frac{\sqrt{5}}{2}$���жϳ���ECA�ס�DCB��Ȼ�������������εĶ�Ӧ�߳ɱ�������ô𰸣�
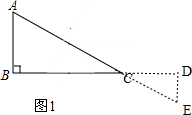
��2�����������������A��D��E��������ֱ����BC���ཻ����BC�ཻ��Ȼ�����ù��ɶ����ֱ���⼴����ô𰸣�
���  �⣺��1���ٵ���=0��ʱ����Rt��ABC�У���B=90�㣬
�⣺��1���ٵ���=0��ʱ����Rt��ABC�У���B=90�㣬
��AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{��8��2��}^{2}+{8}^{2}}$=4$\sqrt{5}$��
�ߵ�D��E�ֱ��DZ�BC��AC���е㣬
��AE=4$\sqrt{5}$��2=2$\sqrt{5}$��BD=8��2=4��
��$\frac{AE}{BD}$=$\frac{2\sqrt{5}}{4}$=$\frac{\sqrt{5}}{2}$��
����ͼ1������=180��ʱ����Rt��ABC�У���B=90�㣬
��AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{��8��2��}^{2}+{8}^{2}}$=4$\sqrt{5}$��
�ߵ�D��E�ֱ��DZ�BC��AC���е㣬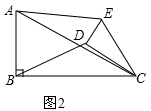
��CD=4��CE=2$\sqrt{5}$��
��AE=4$\sqrt{5}$+2$\sqrt{5}$=6$\sqrt{5}$��BD=8+4=12��
��$\frac{AE}{BD}$=$\frac{6\sqrt{5}}{12}$=$\frac{\sqrt{5}}{2}$��
�۲��룺��0��ܦ���360��ʱ��AE��BD�ı�ֵ�Ƕ�ֵ��
��ͼ2����0��ܦ���360��ʱ��$\frac{AE}{BD}$�Ĵ�Сû�б仯��
�ߡ�ECD=��ACB��
���ECA=��DCB��
�֡�$\frac{EC}{DC}$=$\frac{AC}{BC}$=$\frac{\sqrt{5}}{2}$��
���ECA�ס�DCB��
��$\frac{AE}{DB}$=$\frac{EC}{DC}$=$\frac{\sqrt{5}}{2}$��
��2������ͼ3����AC=4$\sqrt{5}$��CD=4��CD��AD��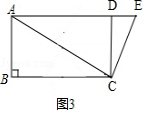
��AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=$\sqrt{��4\sqrt{5}��^{2}-{4}^{2}}$=$\sqrt{80-16}$=8��
��AD=BC��AB=DC����B=90�㣬
���ı���ABCD�Ǿ��Σ�
��BD=AC=5$\sqrt{5}$��
����ͼ4������BD������D��AC�Ĵ��߽�AC�ڵ�Q������B��AC�Ĵ��߽�AC�ڵ�P��
��AC=4$\sqrt{5}$��CD=4��CD��AD��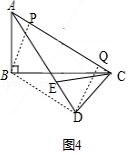
��AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=$\sqrt{��4\sqrt{5}��^{2}-{4}^{2}}$=$\sqrt{80-16}$=8��
�ڡ�ABC�͡�CDA�У�
$\left\{\begin{array}{l}{AB=CD}\\{BC=DA}\\{AC=CA}\end{array}\right.$��
���ABC�ա�CDA��SSS����
��BP=DQ��BP��DQ��PQ��DQ��
���ı���BDQPΪ���Σ�
��BD=PQ=AC-AP-CQ
=4$\sqrt{5}$-$\frac{4}{\sqrt{5}}$-$\frac{4}{\sqrt{5}}$=$\frac{12\sqrt{5}}{5}$��
����������BD�ij�Ϊ4$\sqrt{5}$��$\frac{12\sqrt{5}}{5}$��
���� �������ڼ��α任�ۺ��⣮�����ˡ���ת�����ʡ����������ε��ж��������Լ����ɶ�����֪ʶ��ע�����շ�������˼���Ӧ���ǽ����Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
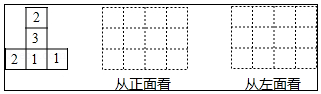
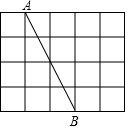 ��ͼ����ÿ��С�����εı߳�Ϊ1�������У���A��B���ڸ���ϣ�
��ͼ����ÿ��С�����εı߳�Ϊ1�������У���A��B���ڸ���ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
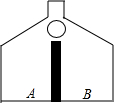 ���ܵ���������ұ����£�
���ܵ���������ұ����£��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ����1�� | ��2�졡 | ����3�� | ����4�� | |
| �������۵���x��Ԫ�� | ��20 | ��30 | ��40 | ��50 |
| ����������y������ | ��30 | ��20 | ��15 | ��12 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
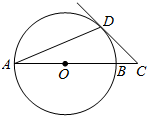 ��ͼ��AB�ǡ�O��ֱ����AD���ң���DAB=22.5�㣬�ӳ�AB����C��ʹ�á�ACD=45�㣬
��ͼ��AB�ǡ�O��ֱ����AD���ң���DAB=22.5�㣬�ӳ�AB����C��ʹ�á�ACD=45�㣬�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
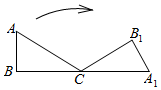 ��ͼ����Rt��ABC�У���A=60�㣬AB=1����Rt��ABC�Ƶ�C��˳ʱ�뷽����ת����A1B1C��λ�ã���A1�պ�����BC���ӳ����ϣ����A�ӿ�ʼ��������������·����Ϊ����������У�$\frac{5}{3}$�У�
��ͼ����Rt��ABC�У���A=60�㣬AB=1����Rt��ABC�Ƶ�C��˳ʱ�뷽����ת����A1B1C��λ�ã���A1�պ�����BC���ӳ����ϣ����A�ӿ�ʼ��������������·����Ϊ����������У�$\frac{5}{3}$�У��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com