
| 1 |
| 2 |
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源:初中几何同步单元练习册 第1册 题型:022
在括号中填上理由.
如图,直线AB,CD被EF所截.

所以∠1=∠2( ).
又因为 ∠1=∠4(已知),
所以 ∠2=∠4(等量代换).
因为 ∠1和∠3互为邻补角.
所以 ∠1+∠3=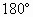 ( ),
( ),
所以 ∠3+∠4=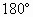 (等量代换).
(等量代换).
所以∠3与∠4互补( ).
查看答案和解析>>
科目:初中数学 来源:2011-2012学年辽宁省鞍山四校七年级3月月考数学试卷(解析版) 题型:选择题
下列说法中,正确的是( )
A.过一点有且只有一条直线与已知直线垂直
B. 如果两个角有公共顶点和一条公共边,且这两个角互补,那么这两个角互为邻补角
C.对顶角相等但不互补,邻补角互补但不相等
D.如果 ,那么M,O,N三点在一条直线上
,那么M,O,N三点在一条直线上
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com