
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为直径作
为直径作![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 的切线
的切线![]() 交
交![]() 于点
于点![]() ,交
,交![]() 延长线于点
延长线于点![]() .
.
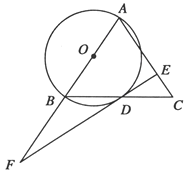
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)BF=![]() .
.
【解析】
试题分析:(1)连接OD、AD,由AB=AC且∠ADB=90°知D是BC的中点,由O是AB中点知OD∥AC,根据OD⊥DE可得;
(2)证△ODF∽△AEF,根据相似的性质即可得答案.
试题解析: (1)连接OD、AD,
∵DE切⊙O于点D,∴OD⊥DE,∵AB是直径,∴∠ADB=90°,∵AB=AC,∴D是BC的中点,
又∵O是AB中点,∴OD∥AC,∴DE⊥AC;
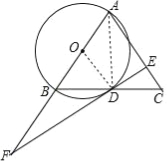
(2)∵AB=10,∴OB=OD=5,由(1)得OD∥AC,∴△ODF∽△AEF,∴![]() ,
,
设BF=x,AE=8,∴![]() ,解得:x=
,解得:x=![]() ,经检验x=
,经检验x=![]() 是原分式方程的根,且符合题意,
是原分式方程的根,且符合题意,
∴BF=![]() .
.


科目:初中数学 来源: 题型:
【题目】综合:
(1)如图1,纸片ABCD中,AD=5,SABCD=15,过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE'的位置,拼成四边形AEE'D,则四边形AEE'D的形状为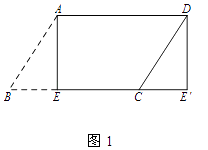
A.平行四边形
B.菱形
C.矩形
D.正方形
(2)如图2,在(1)中的四边形纸片AEE'D中,在EE'上取一点F,使EF=4,剪下△AEF,剪下△AEF,将它平移至△DE'F'的位置,拼成四边形AFF'D.
①求证:四边形AFF'D是菱形;
②求四边形AFF'D的两条对角线的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com