
【题目】(发现)
(1)如图1,在ABCD中,点O是对角线的交点,过点O的直线分别交AD,BC于点E,F.求证:△AOE≌△COF;

(探究)
(2)如图2,在菱形ABCD中,点O是对角线的交点,过点O的直线分别交AD,BC于点E,F,若AC=4,BD=8,求四边形ABFE的面积.
(应用)
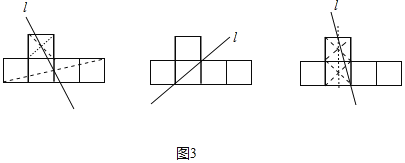
(3)如图3,边长都为1的5个正方形如图摆放,试利用无刻度的直尺,画一条直线平分这5个正方形组成的图形的面积.(要求:保留画图痕迹)
【答案】(1)见解析 (2)8 (3)见解析
【解析】
(1)根据ASA证明三角形全等即可.
(2)证明S四边形ABFE=S△ABC可得结论.
(3)利用中心对称图形的性质以及数形结合的思想解决问题即可(答案不唯一).
(1)【发现】证明:如图1中,∵四边形ABCD是平行四边形,
∴AO=OC,AD∥BC,
∴∠EAO=∠FCO,
在△AOE和△COF中,
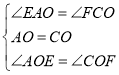 ,
,
∴△AOE≌△COF(ASA).
(2)【探究】解:如图2中,由(1)可知△AOE≌△COF,
∴S△AOE=S△COF,
∴S四边形ABFE=S△ABC,
∵四边形ABCD是菱形,
∴S△ABC=![]() S菱形ABCD,
S菱形ABCD,
∵S菱形ABCD=![]() ACBD=
ACBD=![]() ×4×8=16,
×4×8=16,
∴S四边形ABFE=![]() ×16=8.
×16=8.
(3)【应用】
①找出上面小正方形的对角线交点,以及下面四个小正方形组成的矩形的对角线交点,连接即可;
②连接下面左边数第二个小正方形右上角和左下角的顶点;
③分别找出第二列两个小正方形的对角线交点,并连接,与最上面的小正方形最上面的边交于一点,把这个点与图形底边中点连接即可.
如图3中,直线l即为所求(答案不唯一).


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】下列说法错误的是( )
A. 若AP=BP,则点P是线段的中点 B. 若点C在线段AB上,则AB=AC+BC
C. 若AC+BC>AB,则点C一定在线段AB外 D. 两点之间,线段最短
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知直线y![]() x+3与x轴、y轴分别交于A、B两点,点C在线段OB上,把△ABC沿直线AC折叠,使点B刚好落在x轴上,则点C的坐标是_____.
x+3与x轴、y轴分别交于A、B两点,点C在线段OB上,把△ABC沿直线AC折叠,使点B刚好落在x轴上,则点C的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
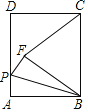
【题目】如图,在矩形ABCD中,AB=5,BC=6,P为AD上一动点,把△ABP沿BP翻折,使点A落在点F处,连接CF,若BF=CF,则AP的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教材的![]() 课题学习
课题学习![]() 要求同学们用一张正三角形纸片折叠成正六边形,小明同学按照如下步骤折叠:
要求同学们用一张正三角形纸片折叠成正六边形,小明同学按照如下步骤折叠:
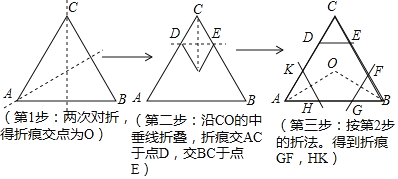
请你根据小明同学的折叠方法,回答以下问题: ![]() 如果设正三角形ABC的边长为a,那么
如果设正三角形ABC的边长为a,那么![]() ______
______ ![]() 用含a的式子表示
用含a的式子表示![]() ;
;
![]() 根据折叠性质可以知道
根据折叠性质可以知道![]() 的形状为______ 三角形;
的形状为______ 三角形;
![]() 请同学们利用
请同学们利用![]() 、
、![]() 的结论,证明六边形KHGFED是一个六边形.
的结论,证明六边形KHGFED是一个六边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,图形
中,图形![]() 的投影矩形定义如下:矩形的两组对边分别平行于
的投影矩形定义如下:矩形的两组对边分别平行于![]() 轴,
轴,![]() 轴,图形
轴,图形![]() 的顶点在矩形的边上或内部,且矩形的面积最小.设矩形的较长的边与较短的边的比为
的顶点在矩形的边上或内部,且矩形的面积最小.设矩形的较长的边与较短的边的比为![]() ,我们称常数
,我们称常数![]() 为图形
为图形![]() 的投影比,如图1,矩形
的投影比,如图1,矩形![]() 为
为![]() 的投影矩形,其投影比
的投影矩形,其投影比![]() .
.
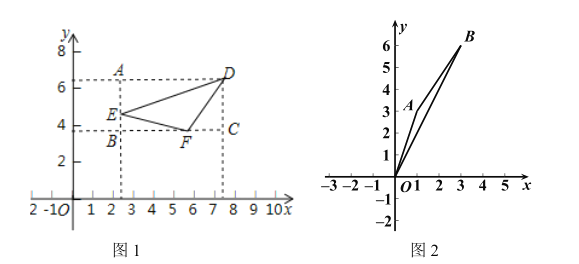
(1)如图2,若点![]() ,则
,则![]() 投影比
投影比![]() 的值为________________;
的值为________________;
(2)已知点![]() ,点
,点![]() ,且
,且![]() 投影比
投影比![]() ,则
,则![]() 点坐标可能是__________(填写序号);
点坐标可能是__________(填写序号);
①![]() ②
②![]() ③
③![]() ④
④![]()
(3)已知点![]() ,在直线
,在直线![]() 上有一点
上有一点![]() 和一动点
和一动点![]() ,且
,且![]() ,是否存在这样的
,是否存在这样的![]() ,使得
,使得![]() 的投影比
的投影比![]() 为定值?若存在,请求出
为定值?若存在,请求出![]() 的范围及定值
的范围及定值![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学校组织的以”垃圾分类 从我做起“的主题知识竞赛活动中,王老师随机抽取了班中参赛的6名学生成绩,若以80分为标准,超过这个分数用正数表示,不足的分数用负数表示,成绩记录如下:-3,+7,-12,+6 , -21 ,+14
(1) 最高分比最低分多多少分?这6名学生平均每人得多少分?
(2) 若规定:成绩高于80分的学生操行分每人加3分,成绩在60~80分的学生操行分每人加2分,成绩在60分以下的学生操行分每人扣1分,那么这6名学生共加操行分多少分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知□ABCD,延长AB到E使BE=AB,连接BD,ED,EC,若ED=AD.
(1)求证:四边形BECD是矩形;
(2)连接AC,若AD=4,CD= 2,求AC的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com