
分析 (1)根据自变量的不同取值范围内不同的函数关系设出不同的函数的解析式,利用待定系数法求得函数的解析式即可;
(2)根据一次函数的增减性和二次函数的最值确定该农产品的最低月份和最低价格即可;
(3)分别计算5个月的平均价格和年平均价格,比较得到结论即可.
解答 解:(1)当1≤x≤7时,设y=kx+m
将点(1,8)、(7,26)分别代入y=kx+m得:
$\left\{\begin{array}{l}{k+m=8}\\{7k+m=26}\end{array}\right.$
解之得:
$\left\{\begin{array}{l}{m=5}\\{k=3}\end{array}\right.$
∴函数的解析式为:y=3x+5
当7≤x≤12时,设y=ax2+bx+c
将点(7,26)、(9,14)、(12,11)代入y=ax2+bx+c
得
$\left\{\begin{array}{l}{49a+7b+c=26}\\{81a+9b+c=14}\\{144a+12b+c=11}\end{array}\right.$
解得:$\left\{\begin{array}{l}{a=1}\\{b=-22}\\{c=131}\end{array}\right.$
∴函数的解析式为y=x2-22x+131;
(2)当1≤x≤7时,y=3x+5为增函数,
当x=1时,y有最小值8.
当7≤x≤12时,y=x2-22x+131=(x-11)2+10,
当x=11时,y有最小值为10.
所以,该农产品月平均价格最低的是1月,最低为8元/千克.
(3)∵1至7月份的月平均价格呈一次函数,
∴x=4时的月平均价格17是前7个月的平均值.
将x=8,x=10和x=11代入y=x2-22x+131
得y=19和y=11,y=10
∴后5个月的月平均价格分别为19、14、11、10、11,
∴年平均价格为$\frac{17×7+19+14+11+10+11}{12}$≈15.3元/千克,
当x=3时,y=14<15.3,
∴4,5,6,7,8这五个月的月平均价格高于年平均价格.
点评 本题考查了二次函数的应用,解决此类问题的关键是从实际问题中整理出函数模型,利用函数的知识解决实际问题.


科目:初中数学 来源: 题型:解答题
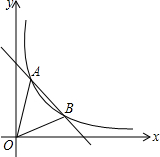 如图,已知A(-1,2),B(m,1)是一次函数y=-x+b的图象和反比例函数y=$\frac{2}{x}$(x>0)的图象的两个交点,连结AO,BO.
如图,已知A(-1,2),B(m,1)是一次函数y=-x+b的图象和反比例函数y=$\frac{2}{x}$(x>0)的图象的两个交点,连结AO,BO.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
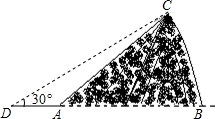 如图,某人在D处测得山顶C的仰角为30°,向前走300米来到山脚A处,测得山坡AC的坡度为i=1:1,求山的高度(不计测角仪的高度,$\sqrt{3}$≈1.73,结果保留整数).
如图,某人在D处测得山顶C的仰角为30°,向前走300米来到山脚A处,测得山坡AC的坡度为i=1:1,求山的高度(不计测角仪的高度,$\sqrt{3}$≈1.73,结果保留整数).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
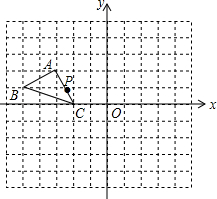 如图,在平面直角坐标系中有三个点A(-3,2)、B(-5,1)、C(-2,0),P(a,b)是△ABC的边AC上一点,△ABC经平移后得到△A1B1C1,点P的对应点为P1(a+6,b+2).
如图,在平面直角坐标系中有三个点A(-3,2)、B(-5,1)、C(-2,0),P(a,b)是△ABC的边AC上一点,△ABC经平移后得到△A1B1C1,点P的对应点为P1(a+6,b+2).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 某天,小明来到体育馆看球赛,进场时,发现门票还在家里,此时离比赛开始还有25分钟,于是立即步行回家取票.同时,他父亲从家里出发骑自行车以他3倍的速度给他送票,两人在途中相遇,相遇后小明立即坐父亲的自行车赶回体育馆.下图中线段AB、OB分别表示父、子俩送票、取票过程中,离体育馆的路程S(米)与所用时间t(分钟)之间的函数关系,骑自行车和步行的速度始终保持不变,则小明在比赛开始前5分钟到达体育馆.
某天,小明来到体育馆看球赛,进场时,发现门票还在家里,此时离比赛开始还有25分钟,于是立即步行回家取票.同时,他父亲从家里出发骑自行车以他3倍的速度给他送票,两人在途中相遇,相遇后小明立即坐父亲的自行车赶回体育馆.下图中线段AB、OB分别表示父、子俩送票、取票过程中,离体育馆的路程S(米)与所用时间t(分钟)之间的函数关系,骑自行车和步行的速度始终保持不变,则小明在比赛开始前5分钟到达体育馆.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com