
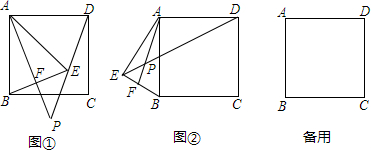
分析 (1)根据正方形的性质得到AD=AB,∠BAD=90°,由AD绕点A顺时针旋转到AE,得到AD=AE,根据等腰三角形的性质得到∠ADE=∠AED=70°,∠BAE=50°,∠FAE=∠FAB=25°,根据三角形的外角的性质即可得到结论;
(2)如图2,过A作AQ⊥DE于Q,于是得到∠PAQ=∠BAQ+∠FAB,根据等腰三角形的性质得到∠FAE=∠BAF,由外角的性质得到∠APQ=∠EAF+∠AEP于是得到∠APQ=∠PAQ=45°,求出PQ=$\frac{\sqrt{2}}{2}$AP,由于PE+PQ=PD-PQ,即PE+$\frac{\sqrt{2}}{2}$AP=PD-$\frac{\sqrt{2}}{2}$AP,于是得到结论;
(3)如图3,过A作AQ⊥DE于Q,则∠AQP=90°,由AD=AE,得到DQ=EQ,∠AEQ=∠ADQ,同理得到∠3=∠FAB,根据外角的性质得到∠APQ=∠3-∠AEQ=∠3-∠ADQ,等量代换得到∠2=90°-∠1-∠ADP=90°-(90°-∠3)-∠AEP=∠3-∠AEP,求得∠2=∠APQ=45°,于是得到PQ=$\frac{\sqrt{2}}{2}$AP,然后由PD+PQ=PE-PQ,即可得到结论:PE=PD+$\sqrt{2}$PA.
解答 解:(1)∵四边形ABCD是正方形,
∴AD=AB,∠BAD=90°,
∵AD绕点A顺时针旋转到AE,
∴AD=AE,
∵∠DAE=40°,
∴∠ADE=∠AED=70°,∠BAE=50°,
∵AF⊥BE,
∴∠FAE=∠FAB=25°,
∴∠P=∠AED-∠PAE=45°;
(2)如图2,过A作AQ⊥DE于Q,则∠PAQ=∠BAQ+∠FAB,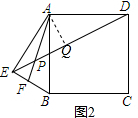 ∵AE=AB,AF⊥BE,
∵AE=AB,AF⊥BE,
∴∠FAE=∠BAF,
∴∠APQ=∠EAF+∠AEP,
∵∠BAD=∠AQP=90°,
∴∠BAQ=∠ADQ,
∵AE=AD,
∴∠ADQ=∠AEP,
∴∠BAQ=∠AEP,
∴∠APQ=∠PAQ=45°,
∴PQ=$\frac{\sqrt{2}}{2}$AP,
∴PE+PQ=PD-PQ,
即PE+$\frac{\sqrt{2}}{2}$AP=PD-$\frac{\sqrt{2}}{2}$AP,
∴PD=$\sqrt{2}$AP+PE;
(3)如图3,过A作AQ⊥DE于Q,则∠AQP=90°,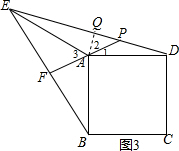 ∵AD=AE,
∵AD=AE,
∴DQ=EQ,∠AEQ=∠ADQ,
∵AE=AB,AF⊥BE,
∴∠3=∠FAB,
∵∠APQ=∠3-∠AEQ=∠3-∠ADQ,
∵∠1+∠FAB=∠FAB+∠ABF=90°,
∴∠1=∠ABF=∠AEF,
∴∠2=90°-∠1-∠ADP=90°-(90°-∠3)-∠AEP=∠3-∠AEP,
∴∠2=∠APQ=45°,
∴PQ=$\frac{\sqrt{2}}{2}$AP,
∴PD+PQ=PE-PQ,
即PD+$\frac{\sqrt{2}}{2}$PA=PE-$\frac{\sqrt{2}}{2}$PA,
∴PE=PD+$\sqrt{2}$PA.
故答案为:PE=PD+$\sqrt{2}$PA.
点评 本题考查了正方形的性质,图形的变换-旋转,等腰三角形的性质,等腰直角三角形的判定和性质,三角形的内角和定理,正确的作出辅助线是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
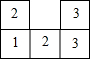 一个几何体由大小相同的立方块搭成,从上面看到的如图所示,其中小正方形中的数字表示在该位置的立方块个数.若允许从该几何体中拿掉部分立方块,使剩下的几何体从正面和上面看的形状相同,则拿掉的立方块数量最多是( )
一个几何体由大小相同的立方块搭成,从上面看到的如图所示,其中小正方形中的数字表示在该位置的立方块个数.若允许从该几何体中拿掉部分立方块,使剩下的几何体从正面和上面看的形状相同,则拿掉的立方块数量最多是( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
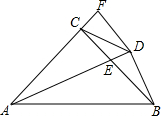 如图,在△ABC中,AC=BC,∠ACB=90°,AE平分∠BAC交BC于E,BD⊥AE于D,DF⊥AC交AC的延长线于F,连接CD,给出四个结论:①∠ADC=45°;②BD=$\frac{1}{2}$AE;③AC+CE=AB;④AB-BC=2FC;其中正确的结论有( )
如图,在△ABC中,AC=BC,∠ACB=90°,AE平分∠BAC交BC于E,BD⊥AE于D,DF⊥AC交AC的延长线于F,连接CD,给出四个结论:①∠ADC=45°;②BD=$\frac{1}{2}$AE;③AC+CE=AB;④AB-BC=2FC;其中正确的结论有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com