
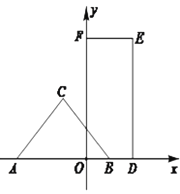
【题目】如图,等腰直角![]() 的斜边
的斜边![]() 在x轴上且长为4,点C在x轴上方.矩形
在x轴上且长为4,点C在x轴上方.矩形![]() 中,点D、F分别落在x、y轴上,边
中,点D、F分别落在x、y轴上,边![]() 长为2,
长为2,![]() 长为4,将等腰直角
长为4,将等腰直角![]() 沿x轴向右平移得等腰直角
沿x轴向右平移得等腰直角![]() .
.
(1)当点![]() 与点D重合时,求直线
与点D重合时,求直线![]() 的解析式;
的解析式;
(2)连接![]() ,
,![]() .当线段
.当线段![]() 和线段
和线段![]() 之和最短时,求矩形
之和最短时,求矩形![]() 和等腰直角
和等腰直角![]() 重叠部分的面积;
重叠部分的面积;
(3)当矩形![]() 和等腰直角
和等腰直角![]() 重叠部分的面积为
重叠部分的面积为![]() 时,求直线
时,求直线![]() 与y轴交点的坐标.(本问直接写出答案即可)
与y轴交点的坐标.(本问直接写出答案即可)
【答案】(1)![]() ;(2)S重合=3;(3)
;(2)S重合=3;(3) .
.
【解析】
(1)由OD=2,AB=4可得B′与D重合时,点O为AB中点,根据等腰直角三角形的性质可得OC⊥AB,OC′=OD,即可得A′、C′的坐标,利用待定系数法即可得A′C′的解析式;(2)根据等腰三角形的性质可得点![]() 在直线
在直线![]() 上移动,由点F与点O关于y=2得出可得当点
上移动,由点F与点O关于y=2得出可得当点![]() ,
,![]() ,
,![]() 在同一条直线上时,
在同一条直线上时,![]()
![]() 最小,根据O、E坐标可得直线OE解析式,即可得出C′坐标,进而可得直线
最小,根据O、E坐标可得直线OE解析式,即可得出C′坐标,进而可得直线![]() 的解析式,可得G点坐标,H点坐标,根据S重合=S△ABC-S△OA′G-S△HDB即可得答案;(3)如图,设OA′=x,根据S△A′OM+S△B′DN=S△ABC-S重合列方程即可求出x的值,即可得直线
的解析式,可得G点坐标,H点坐标,根据S重合=S△ABC-S△OA′G-S△HDB即可得答案;(3)如图,设OA′=x,根据S△A′OM+S△B′DN=S△ABC-S重合列方程即可求出x的值,即可得直线![]() 与
与![]() 轴交点的坐标.
轴交点的坐标.
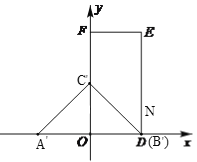
(1)∵点B′与D重合,OD=2,AB=4,
∴OA=OD=2,
∵△A′B′C′是等腰直角三角形,
∴OC′⊥AB,
∴点C′在y轴上,
∴OC′=OD=2,
∴A′(-2,0),C′(0,2)
设A′C′的解析式为y=kx+b,
∴![]() ,
,
解得:![]() ,
,
∴A′C′的解析式为y=x+2.
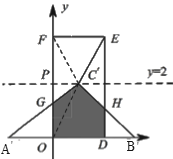
(2)如图,∵△ABC斜边AB上的高为2,
∴点![]() 在直线
在直线![]() 上移动,
上移动,
∵点![]() 和点
和点![]() 关于直线
关于直线![]() 对称.
对称.
∴![]()
∴当点![]() ,
,![]() ,
,![]() 在同一条直线上时,
在同一条直线上时,![]()
![]() 最小,即此时
最小,即此时![]() 取得最小值.
取得最小值.
设直线OE的解析式为y=kx,
∵E(2,4),
∴4=2k,
解得k=2,
∴直线OE的解析式为y=2x,
∴![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,
,
把(1,2)代入,得b=1
∴直线![]() 的解析式为
的解析式为![]() ,
,
当x=0时,y=1,
∴G(0,1),
∴OG=OA′=1,
∴DH=DB′=AB-OA′-OD=1,
∴重叠部分的面积为:![]() .
.
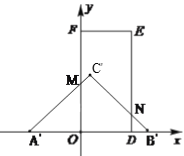
(3)如图,S重合=2.5时,
∴S△A′OM+S△B′DN=S△ABC-S重合=4-2.5=1.5,
设OA′=x,则DB′=2-x(0<x<2),
∵OA′=OM,DB′=DN,
∴![]() x
x![]() x+
x+![]() (2-x)2=1.5,
(2-x)2=1.5,
解得:x=![]() ,
,
∴直线![]() 与
与![]() 轴交点的坐标为(0,
轴交点的坐标为(0,![]() )或(0,
)或(0,![]() ).
).


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于A(1,4),B(4,n)两点.
的图象交于A(1,4),B(4,n)两点.

(1)求反比例函数和一次函数的解析式;
(2)直接写出当x>0时,![]() 的解集.
的解集.
(3)点P是x轴上的一动点,试确定点P并求出它的坐标,使PA+PB最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点.

(1)求该抛物线的解析式;
(2)求该抛物线的对称轴以及顶点坐标;
(3)设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足S△PAB=8,并求出此时P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD和四边形CEFG都是正方形,且AB>CE

(1) 如图1,连接BG、DE,求证:BG=DE
(2) 如图2,如果正方形CEFG绕点C旋转到某一位置恰好使得CG∥BD,BG=BD
① 求∠BDE的度数
② 若正方形ABCD的边长是![]() ,请直接写出正方形CEFG的边长____________
,请直接写出正方形CEFG的边长____________
查看答案和解析>>
科目:初中数学 来源: 题型:
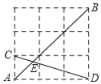
【题目】如图,在由边长为1的小正方形组成的网格中,点A,B,C,D都在这些小正方形的格点上,AB,CD相交于点E,则sin∠AEC的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】y=x2+(1﹣a)x+1是关于x的二次函数,当x的取值范围是1≤x≤3时,y在x=1时取得最大值,则实数a的取值范围是( )
A. a≤﹣5B. a≥5C. a=7D. a≥7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com