
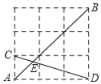
【题目】如图,在由边长为1的小正方形组成的网格中,点A,B,C,D都在这些小正方形的格点上,AB,CD相交于点E,则sin∠AEC的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:初中数学 来源: 题型:
【题目】问题提出;
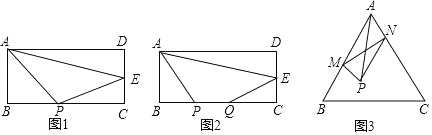
(1)如图1,矩形ABCD,AB=4,BC=8,点E为CD的中点,点P为BC上的动点,CP= 时,△APE的周长最小.
(2)如图2,矩形ABCD,AB=4,BC=8,点E为CD的中点,点P、点Q为BC上的动点,且PQ=2,当四边形APQE的周长最小时,请确定点P的位置(即BP的长)
问题解决;
(3)如图3,某公园计划在一片足够大的等边三角形水域内部(不包括边界)点P处修一个凉亭,设计要求PA长为100米,同时点M,N分别是水域AB,AC边上的动点,连接P、M、N的水上浮桥周长最小时,四边形AMPN的面积最大,请你帮忙算算此时四边形AMPN面积的最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON=α(0<α<90°),A为OM上一点(不与O重合),点A关于直线ON的对称点为B,AB与ON交于点C,P为直线ON上一点(不与O,C重合)将射线PB绕点P顺时针旋转β角,其中2α+β=180°,所得到的射线与直线OM交于点Q.这个问题中,点的位置和角的大小都不确定,在这里我们仅研究两种特殊情况,一般的情况留给同学们深入探索.
(1)如图1,当α=45°时,此时β=90°,若点P在线段OC的延长线上.
①依题意补全图形;
②求∠PQA﹣∠PBA的值;
(2)如图2,当α=60°,点P在线段CO的延长线上时,用等式表示线段OC,OP,AQ之间的数量关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
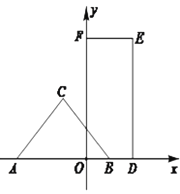
【题目】如图,等腰直角![]() 的斜边
的斜边![]() 在x轴上且长为4,点C在x轴上方.矩形
在x轴上且长为4,点C在x轴上方.矩形![]() 中,点D、F分别落在x、y轴上,边
中,点D、F分别落在x、y轴上,边![]() 长为2,
长为2,![]() 长为4,将等腰直角
长为4,将等腰直角![]() 沿x轴向右平移得等腰直角
沿x轴向右平移得等腰直角![]() .
.
(1)当点![]() 与点D重合时,求直线
与点D重合时,求直线![]() 的解析式;
的解析式;
(2)连接![]() ,
,![]() .当线段
.当线段![]() 和线段
和线段![]() 之和最短时,求矩形
之和最短时,求矩形![]() 和等腰直角
和等腰直角![]() 重叠部分的面积;
重叠部分的面积;
(3)当矩形![]() 和等腰直角
和等腰直角![]() 重叠部分的面积为
重叠部分的面积为![]() 时,求直线
时,求直线![]() 与y轴交点的坐标.(本问直接写出答案即可)
与y轴交点的坐标.(本问直接写出答案即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
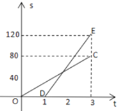
【题目】已知A,B两地相距120千米,甲、乙两人沿同一条公路从A地出发到B地,乙骑自行车,甲骑摩托车,图中DE,OC分别表示甲、乙离开A地的路程s(单位:千米)与时间t(单位:小时)的函数关系的图象,设在这个过程中,甲、乙两人相距y(单位:千米),则y关于t的函数图象是( )
A. 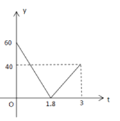 B.
B.  C.
C. 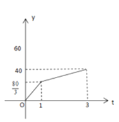 D.
D. 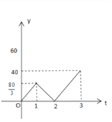
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,AB=AC,点D为BC上一点(不与点B、点C重合),连结AD,以AD为边在右侧作△ADE,DE交AC于点F,其中AD=AE,∠ADE=∠B.
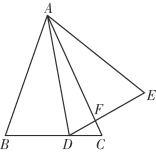
(1)求证:△ABD∽△AEF;
(2)若![]() =
=![]() ,记△ABD的面积为S1,△AEF的面积为S2,求
,记△ABD的面积为S1,△AEF的面积为S2,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰三角形ADC,AD=AC,B是线段DC上的一点,连结AB,且有AB=DB.
(1)求证:△ADB∽△CDA;
(2)若DB=2,BC=3,求AD的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰△ABC的直角边AB=BC=10cm,点P、Q分别从A、C两点同时出发,均以1cm/秒的相同速度作直线运动,已知P沿射线AB运动,Q沿边BC的延长线运动,PQ与直线AC相交于点D.设P点运动时间为t,△PCQ的面积为S.

(1)求出S关于t的函数关系式;
(2)当点P运动几秒时,S△PCQ=S△ABC?
(3)作PE⊥AC于点E,当点P、Q运动时,线段DE的长度是否改变?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四川某特产专卖店销售核桃,其进价为每千克40元,按每千克60元销售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销量可增加20千克.若该专卖店销售这种核桃想要平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折销售?
(3)若该专卖店打算每天获利至少2240元,请你直接写出每千克核桃售价m的取值范围 ________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com