
【题目】问题提出;
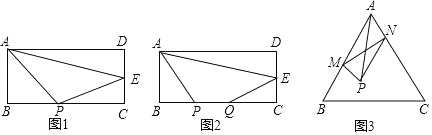
(1)如图1,矩形ABCD,AB=4,BC=8,点E为CD的中点,点P为BC上的动点,CP= 时,△APE的周长最小.
(2)如图2,矩形ABCD,AB=4,BC=8,点E为CD的中点,点P、点Q为BC上的动点,且PQ=2,当四边形APQE的周长最小时,请确定点P的位置(即BP的长)
问题解决;
(3)如图3,某公园计划在一片足够大的等边三角形水域内部(不包括边界)点P处修一个凉亭,设计要求PA长为100米,同时点M,N分别是水域AB,AC边上的动点,连接P、M、N的水上浮桥周长最小时,四边形AMPN的面积最大,请你帮忙算算此时四边形AMPN面积的最大值是多少?
【答案】(1)![]() ;(2)BP=4;(3)
;(2)BP=4;(3)![]() 平方米.
平方米.
【解析】
(1)延长AB到M,使BM=AB,则A和M关于BC对称,连接EM交BC于P,此时AP+EP的值最小,根据勾股定理求出AE长,根据矩形性质得出AB∥CD,推出△ECP∽△MBP,得出比例式,代入即可求出CP长;
(2)点A向右平移2个单位到M,点E关于BC的对称点F,连接MF,交BC于Q,要使四边形APQE的周长最小,只要AP+EQ最小就行,证△MNQ∽△FCQ即可求BP的长;
(3)作点P关于AB的对称点G,作点P关于AC的对称点H,连接GH,交AB,AC于点M,N,此时△PMN的周长最小.S四边形AMPN=S△AGM+S△ANH=S△AGH-S△AMN,即S△AMN的值最小时,S四边形AMPN的值最大.
解:(1):∵四边形ABCD是矩形,
∴∠D=90°=∠ABC,AB=CD=4,BC=AD=8,
∵E为CD中点,
∴DE=CE=2,
在Rt△ADE中,由勾股定理得:AE=![]() =
=![]() =2
=2![]() ,
,
即△APE的边AE的长一定,
要△APE的周长最小,只要AP+PE最小即可,
延长AB到M,使BM=AB=4,则A和M关于BC对称,
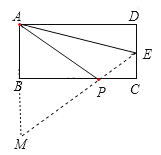
连接EM交BC于P,此时AP+EP的值最小,
∵四边形ABCD是矩形,
∴AB∥CD,
∴△ECP∽△MBP,
∴![]()
∴![]()
∴CP=![]()
故答案为:![]()
(2)点A向右平移2个单位到M,点E关于BC的对称点F,连接MF,交BC于Q,
此时MQ+EQ最小,
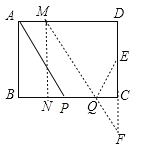
∵PQ=3,DE=CE=2,AE=2![]() ,
,
∴要使四边形APQE的周长最小,只要AP+EQ最小就行,
即AP+EQ=MQ+EQ,过M作MN⊥BC于N,
∴MN∥CD
∴△MNQ∽△FCQ,
∴![]()
∴![]()
∴NQ=4
∴BP=BQ﹣PQ=4+2﹣2=4
(3)如图,作点P关于AB的对称点G,作点P关于AC的对称点H,连接GH,交AB,AC于点M,N,此时△PMN的周长最小.
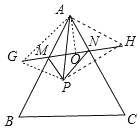
∴AP=AG=AH=100米,∠GAM=∠PAM,∠HAN=∠PAN,
∵∠PAM+∠PAN=60°,
∴∠GAH=120°,且AG=AH,
∴∠AGH=∠AHG=30°,
过点A作AO⊥GH,
∴AO=50米,HO=GO=50![]() 米,
米,
∴GH=100![]() 米,
米,
∴S△AGH=![]() GH×AO=2500
GH×AO=2500![]() 平方米,
平方米,
∵S四边形AMPN=S△AGM+S△ANH=S△AGH﹣S△AMN,
∴S△AMN的值最小时,S四边形AMPN的值最大,
∴MN=GM=NH=![]() 时
时
∴S四边形AMPN=S△AGH﹣S△AMN=2500![]() ﹣
﹣![]() =
=![]() 平方米.
平方米.


科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的y与x的部分对应值如表:则下列判断中正确的是( )
x | … | ﹣1 | 0 | 1 | 3 | … |
y | … | ﹣3 | 1 | 3 | 1 | … |
A. 抛物线开口向上B. 抛物线与y轴交于负半轴
C. 当x=4时,y>0D. 方程ax2+bx+c=0的正根在3与4之间
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A,B的坐标分别为(4,0),(3,2).
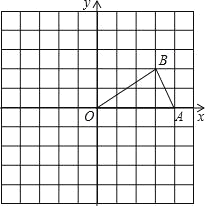
(1)画出△AOB关于原点O对称的图形△COD;
(2)将△AOB绕点O按逆时针方向旋转90°得到△EOF,画出△EOF;
(3)点D的坐标是 ,点F的坐标是 ,此图中线段BF和DF的关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于A(1,4),B(4,n)两点.
的图象交于A(1,4),B(4,n)两点.

(1)求反比例函数和一次函数的解析式;
(2)直接写出当x>0时,![]() 的解集.
的解集.
(3)点P是x轴上的一动点,试确定点P并求出它的坐标,使PA+PB最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某中学去年中招体育考试中女生”一分钟跳绳”项目的成绩情况,从中抽取部分女生的成绩,绘制出如图所示的频数分布直方图(从左到右依次为第一组到第六组,每小组含最小值,不含最大值)和扇形统计图,请根据下列统计图中提供的信息解决下列问题
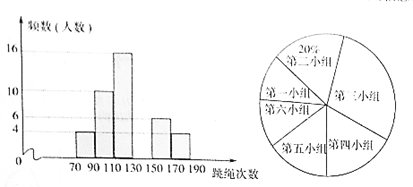
(1)本次抽取的女生总人数为 第六小组人数占总人数的百分比为 请补全频数分布直方图;
(2)题中样本数据的中位数落在第 组内;
(3)若“一分钟跳绳”不低于130次的成绩为优秀,这个学校九年级共有女生560人,请估计该校九年级女生“一分钟跳绳”成绩的优秀人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,A(1,2),B(3,4),C(4,1),连接AB、BC、CA,平移△ABC得到△DEF,其中A点与D点对应,B点与E点对应,C点与F点对应。
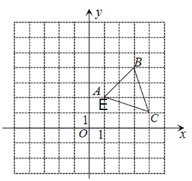
(1)使E与A重合,画出△DEF,并写出F的坐标;
(2)若将△ABC向左平移![]() 个单位,使得到的△DEF的顶点D、F分别位于
个单位,使得到的△DEF的顶点D、F分别位于![]() 轴两侧,求
轴两侧,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在由边长为1的小正方形组成的网格中,点A,B,C,D都在这些小正方形的格点上,AB,CD相交于点E,则sin∠AEC的值为( )
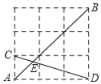
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com