
【题目】在平面直角坐标系中,A(1,2),B(3,4),C(4,1),连接AB、BC、CA,平移△ABC得到△DEF,其中A点与D点对应,B点与E点对应,C点与F点对应。
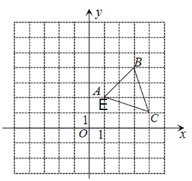
(1)使E与A重合,画出△DEF,并写出F的坐标;
(2)若将△ABC向左平移![]() 个单位,使得到的△DEF的顶点D、F分别位于
个单位,使得到的△DEF的顶点D、F分别位于![]() 轴两侧,求
轴两侧,求![]() 的取值范围。
的取值范围。
科目:初中数学 来源: 题型:
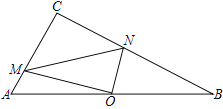
【题目】在Rt△ABC中,∠C=90°,点O是AB的中点,M、N分别在边AC、BC上,OM⊥ON,连MN,AC=4,BC=8.设AM=a,BN=b,MN=c
(1) 求证:a2+b2=c2
(2) ① 若a=1,求b;② 探究a与b之间的函数关系式
(3) △CMN的面积的最大值为__________(不写解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了创建“最美校园图书屋”,新购买了一批图书,其中科普类图书平均每本书的价格是文学类图书平均每本书价格的1.2倍.已知学校用12000元购买文学类图书的本数比用这些钱购买科普类图书的本数多100本,那么学校购买文学类图书平均每本书的价格是多少元?设学校购买文学类图书平均每本书的价格是x元,则下面所列方程中正确的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
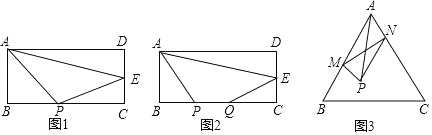
【题目】问题提出;
(1)如图1,矩形ABCD,AB=4,BC=8,点E为CD的中点,点P为BC上的动点,CP= 时,△APE的周长最小.
(2)如图2,矩形ABCD,AB=4,BC=8,点E为CD的中点,点P、点Q为BC上的动点,且PQ=2,当四边形APQE的周长最小时,请确定点P的位置(即BP的长)
问题解决;
(3)如图3,某公园计划在一片足够大的等边三角形水域内部(不包括边界)点P处修一个凉亭,设计要求PA长为100米,同时点M,N分别是水域AB,AC边上的动点,连接P、M、N的水上浮桥周长最小时,四边形AMPN的面积最大,请你帮忙算算此时四边形AMPN面积的最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市草莓种植大户,需将一批草莓运往省内某地,运输可选用A、B两种运输方式的一种,都可在同一地点将这批草莓上车沿同一条公路运往目的地,在运输过程中的有关数据如下:
项目 运输方式 | 装卸时间(小时) | 装卸费用(元) | 途中平均速度(千米/时) | 途中平均运费(元/千米) |
A | 2 | 1100 | 80 | 8 |
B | 3 | 1500 | 100 | 7 |
若这批草莓在运输过程(包括装卸时间)中,损耗为160元/时,设运输路程为![]() (
(![]() )千米,A种运输方式所需总费用为
)千米,A种运输方式所需总费用为![]() 元,B种运输方式所需总费用为
元,B种运输方式所需总费用为![]() 元.(总费用=运输过程损耗费用+运费+装卸费用)
元.(总费用=运输过程损耗费用+运费+装卸费用)
(1)分别求出![]() 、
、![]() 与
与![]() 的关系式;
的关系式;
(2)应采用哪种运输方式,才使运输所需总费用最小?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的方程![]() 有两个不相等的实数根.
有两个不相等的实数根.
(1)求m的取值范围;
(2)是否存在实数m,使方程的两个实数根的倒数和等于0?若存在,求出m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
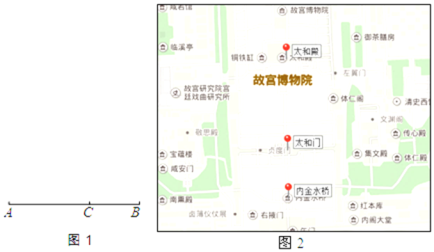
【题目】如图1,在线段AB上找一点C,C把AB分为AC和CB两段,其中BC是较小的一段,如果BCAB=AC2,那么称线段AB被点C黄金分割.为了增加美感,黄金分割经常被应用在绘画、雕塑、音乐、建筑等艺术领域.如图2,在“附中博识课程中”,小白菜们沿着紫禁城的中轴线,从内金水桥走到了太和殿,领略了古代建筑的宏伟.太和门位于太和殿与内金水桥之间靠近内金水桥的一侧,三个建筑的位置关系满足黄金分割.已知太和殿到内金水桥的距离约为100丈,设太和门到太和殿之间的距离为x丈,要求x,则可列方程为________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,AB=AC,点D为BC上一点(不与点B、点C重合),连结AD,以AD为边在右侧作△ADE,DE交AC于点F,其中AD=AE,∠ADE=∠B.
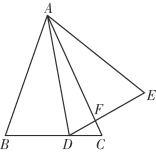
(1)求证:△ABD∽△AEF;
(2)若![]() =
=![]() ,记△ABD的面积为S1,△AEF的面积为S2,求
,记△ABD的面积为S1,△AEF的面积为S2,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com