
【题目】在Rt△ABC中,∠C=90°,点O是AB的中点,M、N分别在边AC、BC上,OM⊥ON,连MN,AC=4,BC=8.设AM=a,BN=b,MN=c
(1) 求证:a2+b2=c2
(2) ① 若a=1,求b;② 探究a与b之间的函数关系式
(3) △CMN的面积的最大值为__________(不写解答过程)
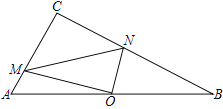
【答案】(1)见解析;(2)①4.5,②a+2b=10;(3)6.
【解析】
(1)过点B作BE∥AC交MO的延长线于E,连接NE,由△AOM≌△BOE,得MO=OE,AM=BE=a,根据垂直平分线的性质得NM=NE,然后证明△NBE是直角三角形即可;
(2)①根据MN2=CM2+CN2,a2+b2=c2,列出方程即可解决;
②方法类似①,由c2=(4a)2+(8b)2=a2+b2可得;
(3)根据S△CMN=![]() (4a)(8b)=b2+11b24,利用二次函数的性质解决问题.
(4a)(8b)=b2+11b24,利用二次函数的性质解决问题.
解:(1)证明:如图,过点B作BE∥AC交MO的延长线于E,连接NE.
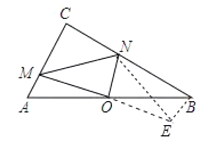
∵AM∥BE,
∴∠A=∠OBE,
在△AOM和△BOE中,∠A=∠OBE,AO=BO,∠AOM=∠BOE,
∴△AOM≌△BOE,
∴MO=OE,AM=BE=a,
∵OM⊥ON,
∴MN=NE=c,
∵∠C=90°
∴∠A+∠ABC=90°,
∴∠OBE+∠ABC=90°,
∴∠EBN=90°,
∴NE2=BN2+BE2,
∵NE=c,BE=a,BN=b,
∴a2+b2=c2;
(2)①在Rt△MNC中,MN2=CM2+CN2,
∴c2=(4a)2+(8b)2,∵a=1,a2+b2=c2,
∴1+b2=9+(8b)2,
∴b=4.5;
②∵c2=(4a)2+(8b)2=a2+b2,
∴a+2b=10.
(3)S△CMN=![]() (4a)(8b)=-b2+11b-24=
(4a)(8b)=-b2+11b-24=![]() ,
,
∵a+2b=10,
∵3≤b≤5,
∴当b=5时,S△CMN最大值=6.
故答案为6.


科目:初中数学 来源: 题型:
【题目】如图所示,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.
(1)求证:△ACE≌△BCD;
(2)若AD=5,BD=12,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应市委市政府提出的建设“绿色襄阳”的号召,我市某单位准备将院内一块长30m,宽20m的长方形空地,建成一个矩形花园.要求在花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草,如图所示,要使种植花草的面积为532m2,那么小道进出口的宽度应为多少米?(注:所有小道进出口的宽度相等,且每段小道均为平行四边形)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是半圆
是半圆![]() 的直径,射线
的直径,射线![]() 于点
于点![]() ,点
,点![]() 是射线
是射线![]() 上一动点,连接
上一动点,连接![]() ,将
,将![]() 沿
沿![]() 翻折,点
翻折,点![]() 落在点
落在点![]() 处,过点
处,过点![]() 作直线
作直线![]() .
.

(1)当![]() 时,求证:
时,求证:![]() 是半圆
是半圆![]() 的切线;
的切线;
(2)点![]() 在射线
在射线![]() 上继续向上运动,直线
上继续向上运动,直线![]() 是否会再次与半圆
是否会再次与半圆![]() 相切,若相切,求出
相切,若相切,求出![]() 的度数;若不相切,请说明理由.
的度数;若不相切,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的y与x的部分对应值如表:则下列判断中正确的是( )
x | … | ﹣1 | 0 | 1 | 3 | … |
y | … | ﹣3 | 1 | 3 | 1 | … |
A. 抛物线开口向上B. 抛物线与y轴交于负半轴
C. 当x=4时,y>0D. 方程ax2+bx+c=0的正根在3与4之间
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).

(1)平移△ABC,若点A的对应点A1的坐标为(0,﹣4),画出平移后对应的△A1B1C1,并写出B1,C1的坐标;
(2)将△ABC以点C为旋转中心逆时针旋转90°,画出旋转后对应的△A2B2C2,并写出B2,C2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的对称轴为
的对称轴为![]() ,与
,与![]() 轴的一个交点在
轴的一个交点在![]() 和
和![]() 之间,其部分图象如图所示,则下列结论:(1)
之间,其部分图象如图所示,则下列结论:(1)![]() :(2)
:(2)![]() ;(3)
;(3)![]() (
(![]() 为任意实数);(4)
为任意实数);(4)![]() ;5)点
;5)点![]()
![]()
![]() 是该抛物线上的点,且
是该抛物线上的点,且![]() ,其中正确结论的个数是( )
,其中正确结论的个数是( )

A. 2B. 3C. 4D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
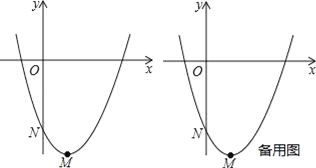
【题目】已知抛物线l:y=ax2+bx+c(a,b,c均不为0)的顶点为M,与y轴的交点为N,我们称以N为顶点,对称轴是y轴且过点M的抛物线为抛物线l的衍生抛物线,直线MN为抛物线l的衍生直线.
(1)如图,抛物线y=x2﹣2x﹣3的衍生抛物线的解析式是 ,衍生直线的解析式是 ;
(2)若一条抛物线的衍生抛物线和衍生直线分别是y=﹣2x2+1和y=﹣2x+1,求这条抛物线的解析式;
(3)如图,设(1)中的抛物线y=x2﹣2x﹣3的顶点为M,与y轴交点为N,将它的衍生直线MN先绕点N旋转到与x轴平行,再沿y轴向上平移1个单位得直线n,P是直线n上的动点,是否存在点P,使△POM为直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,A(1,2),B(3,4),C(4,1),连接AB、BC、CA,平移△ABC得到△DEF,其中A点与D点对应,B点与E点对应,C点与F点对应。
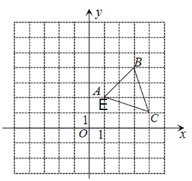
(1)使E与A重合,画出△DEF,并写出F的坐标;
(2)若将△ABC向左平移![]() 个单位,使得到的△DEF的顶点D、F分别位于
个单位,使得到的△DEF的顶点D、F分别位于![]() 轴两侧,求
轴两侧,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com