
【题目】某市草莓种植大户,需将一批草莓运往省内某地,运输可选用A、B两种运输方式的一种,都可在同一地点将这批草莓上车沿同一条公路运往目的地,在运输过程中的有关数据如下:
项目 运输方式 | 装卸时间(小时) | 装卸费用(元) | 途中平均速度(千米/时) | 途中平均运费(元/千米) |
A | 2 | 1100 | 80 | 8 |
B | 3 | 1500 | 100 | 7 |
若这批草莓在运输过程(包括装卸时间)中,损耗为160元/时,设运输路程为![]() (
(![]() )千米,A种运输方式所需总费用为
)千米,A种运输方式所需总费用为![]() 元,B种运输方式所需总费用为
元,B种运输方式所需总费用为![]() 元.(总费用=运输过程损耗费用+运费+装卸费用)
元.(总费用=运输过程损耗费用+运费+装卸费用)
(1)分别求出![]() 、
、![]() 与
与![]() 的关系式;
的关系式;
(2)应采用哪种运输方式,才使运输所需总费用最小?
【答案】(1)yA=10x+1420;yB=8.6x+1980;(2)当运输路程为400千米时选哪个都行;当运输路程大于400千米时选B更合适;当运输路程小于400千米时选A更合适.
【解析】
(1)可根据总运费=(装卸的时间+行驶的时间)×草莓的损耗+行驶的费用+装卸的费用.来列出A,B的总运费和运输路程的关系式;
(2)可将(1)中得出的式子进行比较,得出最省钱的方案.
(1)由题意得:
yA=(2+![]() )×160+8x+1100=10x+1420
)×160+8x+1100=10x+1420
yB=(3+![]() )×160+7x+1500=8.6x+1980;
)×160+7x+1500=8.6x+1980;
(2)①当yA=yB时,10x+1420=8.6x+1980,x=400,当运输路程为400千米时选哪个都行.
②当yA>yB时,10x+1420>8.6x+1980,x>400,当运输路程大于400千米时选B更合适.
③当yA<yB时,10x+1420<8.6x+1980,x<400,当运输路程小于400千米时选A更合适.


科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).

(1)平移△ABC,若点A的对应点A1的坐标为(0,﹣4),画出平移后对应的△A1B1C1,并写出B1,C1的坐标;
(2)将△ABC以点C为旋转中心逆时针旋转90°,画出旋转后对应的△A2B2C2,并写出B2,C2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
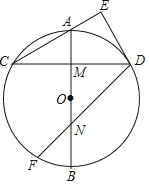
【题目】如图,AB是⊙O的直径,M是OA的中点,弦CD⊥AB于点M,过点D作DE⊥CA交CA的延长线于点E.
(1)连接AD,则∠OAD= °;
(2)求证:DE与⊙O相切;
(3)点F在![]() 上,∠CDF=45°,DF交AB于点N.若DE=3,求FN的长.
上,∠CDF=45°,DF交AB于点N.若DE=3,求FN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O是以AB为直径的△ABC的外接圆,过点A作⊙O的切线交OC的延长线于点D,交BC的延长线于点E.
(1)求证:∠DAC=∠DCE;
(2)若AB=2,sin∠D=![]() ,求AE的长.
,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,A(1,2),B(3,4),C(4,1),连接AB、BC、CA,平移△ABC得到△DEF,其中A点与D点对应,B点与E点对应,C点与F点对应。
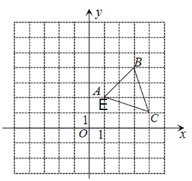
(1)使E与A重合,画出△DEF,并写出F的坐标;
(2)若将△ABC向左平移![]() 个单位,使得到的△DEF的顶点D、F分别位于
个单位,使得到的△DEF的顶点D、F分别位于![]() 轴两侧,求
轴两侧,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx﹣3(a≠0)与直线y=kx+c(k≠0)相交于A(﹣1,0)、B(2,﹣3)两点,且抛物线与y轴交于点C.
(1)求抛物线的解析式;
(2)求出C、D两点的坐标
(3)在第四象限抛物线上有一点P,若△PCD是以CD为底边的等腰三角形,求出点P的坐标.
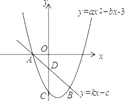
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明想用镜子测量一棵松树的高度,但因树旁有一条河,不能测量镜子与树之间的距离,于是他两次利用镜子,如图所示,第一次他把镜子放在C点,人在F点时正好在镜子中看到树尖A;第二次把镜子放在D点,人在G点正好看到树尖A.已知小明的眼睛距离地面1.70m,量得CD=12m,CF=1.8m,DH=3.8m.请你求出松树的高.
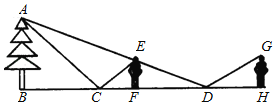
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,Rt△ABC中,∠ACB=90°,点D为AB边上的动点(点D不与点A,点B重合),过点D作ED⊥CD交直线AC于点E,已知∠A=30°,AB=4cm,在点D由点A到点B运动的过程中,设AD=xcm,AE=ycm.
小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小东的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
x/cm | … |
| 1 |
| 2 |
| 3 |
| … |
y/cm | … | 0.4 | 0.8 | 1.0 |
| 1.0 | 0 | 4.0 | … |
(说明:补全表格时相关数值保留一位小数)
(2)在如图2的平面直角坐标系xOy中,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)结合画出的函数图象,解决问题:当AE=![]() AD时,AD的长度约为 cm.
AD时,AD的长度约为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
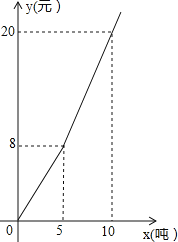
【题目】浙江实施“五水共治“以来,越来越重视节约用水,某地对居民用水按阶梯水价方式进行收费,人均月生活用水收费标准如图所示,图中x表示人均月生活用水的吨数,y表示收取的人均月生活用水费(元),请根据图象信息,回答下列问题.
(1)请写出y与x的函数关系式;
(2)若某个家庭有5人,响应节水号召,计划控制1月份的生活用水费不超过76元,则该家庭这个月最多可以用多少吨水?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com