
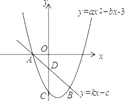
【题目】抛物线y=ax2+bx﹣3(a≠0)与直线y=kx+c(k≠0)相交于A(﹣1,0)、B(2,﹣3)两点,且抛物线与y轴交于点C.
(1)求抛物线的解析式;
(2)求出C、D两点的坐标
(3)在第四象限抛物线上有一点P,若△PCD是以CD为底边的等腰三角形,求出点P的坐标.
【答案】(1)y=x2﹣2x﹣3;(2)C(0,﹣3),D(0,﹣1);(3)P(1+![]() ,﹣2).
,﹣2).
【解析】
(1)把A(﹣1,0)、B(2,﹣3)两点坐标代入y=ax2+bx﹣3可得抛物线解析式.
(2)当x=0时可求C点坐标,求出直线AB解析式,当x=0可求D点坐标.
(3)由题意可知P点纵坐标为﹣2,代入抛物线解析式可求P点横坐标.
解:(1)把A(﹣1,0)、B(2,﹣3)两点坐标代入
y=ax2+bx﹣3可得 ![]()
解得![]()
∴y=x2﹣2x﹣3
(2)把x=0代入y=x2﹣2x﹣3中可得y=﹣3∴C(0,﹣3)
设y=kx+b,把A(﹣1,0)、B(2,﹣3)两点坐标代入
![]()
解得![]()
∴y=﹣x﹣1
∴D(0,﹣1)
(3)由C(0,﹣3),D(0,﹣1)可知CD的垂直平分线经过(0,﹣2)
∴P点纵坐标为﹣2,
∴x2﹣2x﹣3=﹣2
解得:x=1±![]() ,∵x>0∴x=1+
,∵x>0∴x=1+![]() .
.
∴P(1+![]() ,﹣2)
,﹣2)


 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:
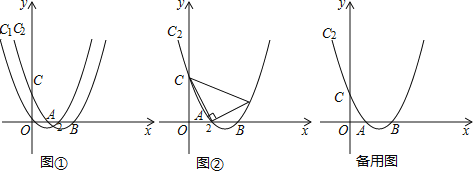
【题目】如图![]() ,抛物线
,抛物线![]() :
:![]() 经过原点
经过原点![]() ,与x轴的另一个交点为
,与x轴的另一个交点为![]() ,将抛物线
,将抛物线![]() 向右平移
向右平移![]() 个单位得到抛物线
个单位得到抛物线![]() ,
,![]() 交x轴于A、B两点
交x轴于A、B两点![]() 点A在点B的左边
点A在点B的左边![]() ,交y轴于点C.
,交y轴于点C.
![]() 求抛物线
求抛物线![]() 的解析式.
的解析式.
![]() 如图
如图![]() ,当
,当![]() 时,连接AC,过点A做
时,连接AC,过点A做![]() 交抛物线
交抛物线![]() 于点D,连接CD.
于点D,连接CD.
![]() 求抛物线
求抛物线![]() 的解析式.
的解析式.
![]() 直接写出点D的坐标为______.
直接写出点D的坐标为______.
![]() 若抛物线
若抛物线![]() 的对称轴上存在点P,使
的对称轴上存在点P,使![]() 为等边三角形,请直接写出此时m的值.
为等边三角形,请直接写出此时m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
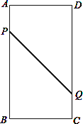
【题目】如图,在矩形ABCD中,AB=16cm,BC=6cm,点P从A出发沿AB以3cm/s的速度向点B移动,一直到达点B为止;同时,点Q从点C出发沿以2cm/s的速度向点D移动.经过多长时间P、Q两点的距离是10?
查看答案和解析>>
科目:初中数学 来源: 题型:
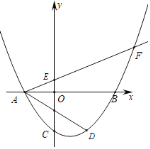
【题目】如图,在平面直角坐标系xOy中,已知抛物线![]() 与x轴交于点A、
与x轴交于点A、![]() 在B左侧
在B左侧![]() ,与y轴交于点C,经过点A的射线AF与y轴正半轴相交于点E,与抛物线的另一个交点为F,
,与y轴交于点C,经过点A的射线AF与y轴正半轴相交于点E,与抛物线的另一个交点为F,![]() ,点D是点C关于抛物线对称轴的对称点,点P是y轴上一点,且
,点D是点C关于抛物线对称轴的对称点,点P是y轴上一点,且![]() ,则点P的坐标是______.
,则点P的坐标是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过点(﹣1,0),对称轴为直线l,则下列结论:①abc>0;②a+b+c>0;③a+c>0;④a+b>0,正确的是( )

A. ①②④B. ②④C. ①③D. ①④
查看答案和解析>>
科目:初中数学 来源: 题型:
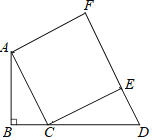
【题目】如图,四边形ACEF为正方形,以AC为斜边作Rt△ABC,∠B=90°,AB=4,BC=2,延长BC至点D,使CD=5,连接DE.
(1)求正方形的边长;
(2)求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
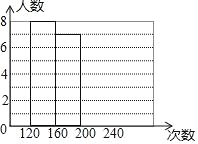
【题目】某体育老师随机抽取了九年级甲、乙两班部分学生进行一分钟跳绳的测试,并对成绩进行统计分析,绘制了频数分布表和统计图,请你根据图表中的信息完成下列问题:
分组 | 频数 | 频率 |
第一组(0≤x<120) | 3 | 0.15 |
第二组(120≤x<160) | 8 | a |
第三组(160≤x<200) | 7 | 0.35 |
第四组(200≤x<240) | b | 0.1 |
(1)频数分布表中a=____,b=_____,并将统计图补充完整;
(2)如果该校九年级共有学生360人,估计跳绳能够一分钟完成160或160次以上的学生有多少人?
(3)已知第一组中有两个甲班学生,第四组中只有一个甲班学生,老师随机从这两个组中各选一名学生谈测试体会,则所选两人正好都是甲班学生的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
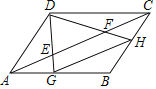
【题目】如图,E,F是平行四边形ABCD对角线AC上两点,AE=CF=![]() AC.连接DE,DF并延长,分别交AB,BC于点G,H,连接GH,则
AC.连接DE,DF并延长,分别交AB,BC于点G,H,连接GH,则![]() 的值为( )
的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图抛物线y=ax2+bx+c的对称轴为直线x=1,且过点(3,0),下列结论:①abc>0;②a﹣b+c<0;③2a+b>0;④b2﹣4ac>0;正确的有( )个.
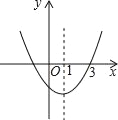
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com