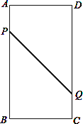
【题目】如图，在矩形ABCD中，AB=16cm，BC=6cm，点P从A出发沿AB以3cm/s的速度向点B移动，一直到达点B为止；同时，点Q从点C出发沿以2cm/s的速度向点D移动．经过多长时间P、Q两点的距离是10？
名校课堂系列答案科目：初中数学 来源： 题型：
【题目】太阳能光伏发电因其清洁、安全、便利、高效等特点，已成为世界各国普遍关注和重点发展的新兴产业，如图是太阳能电池板支撑架的截面图，其中的粗线表示支撑角钢，太阳能电池板与支撑角钢AB的长度相同，均为300cm，AB的倾斜角为
，BE=CA=50cm，支撑角钢CD，EF与底座地基台面接触点分别为D，F，CD垂直于地面，
于点E．两个底座地基高度相同（即点D，F到地面的垂直距离相同），均为30cm，点A到地面的垂直距离为50cm，求支撑角钢CD和EF的长度各是多少cm（结果保留根号）
查看答案和解析>>
科目：初中数学 来源： 题型：
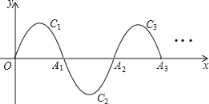
【题目】如图，一段抛物线：y＝﹣x（x﹣2）（0≤x≤2）记为C1，它与x轴交于点O，A1；将C1绕点A1旋转180°得C2，交x轴于点A2；将C2绕点A2旋转180°得C3，交x轴于点A3…如此进行下去，则C2019的顶点坐标是_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
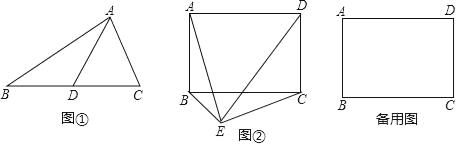
【题目】小儒在学习了定理“直角三角形斜边上的中线等于斜边的一半”之后做了如下思考：
（1）他认为该定理有逆定理，即“如果一个三角形某条边上的中线等于该边长的一半，那么这个三角形是直角三角形”应该成立，你能帮小儒证明一下吗？如图①，在△ABC中，AD是BC边上的中线，若AD＝BD＝CD，求证：∠BAC＝90°．
（2）接下来，小儒又遇到一个问题：如图②，已知矩形ABCD，如果在矩形外存在一点E，使得AE⊥CE，求证：BE⊥DE，请你作出证明，可以直接用到第（1）问的结论．
（3）在第（2）问的条件下，如果△AED恰好是等边三角形，直接用等式表示出此时矩形的两条邻边AB与BC的数量关系．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，⊙P的圆心P(m，n)在抛物线y＝
上．
(1)写出m与n之间的关系式；
(2)当⊙P与两坐标轴都相切时，求出⊙P的半径；
(3)若⊙P的半径是8，且它在x轴上截得的弦MN，满足0≤MN≤2
时，求出m、n的范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】反比例函数y＝
的图象如图所示，以下结论：①常数m＜﹣2；②若A（﹣1，h），B（2，k）在图象上，则h＜k；③y随x的增大而减小；④若P（x，y）在图象上，则P'（﹣x，﹣y）也在图象上．其中正确的是（ ）
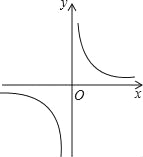
A. ①②B. ③④C. ②③D. ②④
查看答案和解析>>
科目：初中数学 来源： 题型：
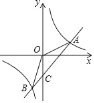
【题目】如图，一次函数y＝ax+b（a≠0）的图象与反比例函数y＝
（k≠0）的图象相交于A、B两点且点A的坐标为（3，1），点B的坐标（﹣1，n）．
（1）分别求两个函数的解析式；
（2）求△AOB的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
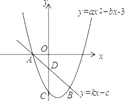
【题目】抛物线y＝ax2+bx﹣3（a≠0）与直线y＝kx+c（k≠0）相交于A（﹣1，0）、B（2，﹣3）两点，且抛物线与y轴交于点C．
（1）求抛物线的解析式；
（2）求出C、D两点的坐标
（3）在第四象限抛物线上有一点P，若△PCD是以CD为底边的等腰三角形，求出点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在Rt△ABC和Rt△DEF中，∠C＝∠F＝90°，下列条件中不能判定这两个三角形相似的是( )
A. ∠A＝55°，∠D＝35°
B. AC＝9，BC＝12，DF＝6，EF＝8
C. AC＝3，BC＝4，DF＝6，DE＝8
D. AB＝10，AC＝8，DE＝15，EF＝9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
