
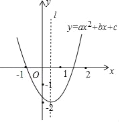
【题目】如图,抛物线y=ax2+bx+c经过点(﹣1,0),对称轴为直线l,则下列结论:①abc>0;②a+b+c>0;③a+c>0;④a+b>0,正确的是( )

A. ①②④B. ②④C. ①③D. ①④
【答案】D
【解析】
由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴进行推理,进而对所得结论进行判断.
解:①抛物线的对称轴位于y轴的右侧,则a、b异号,即ab<0.
抛物线与y轴交于负半轴,则c<0.
所以abc>0.
故正确;
②如图所示,当x=1时,y<0,即a+b+c<0,
故错误;
③由图可知,当x=﹣1时,y=0,即a﹣b+c=0,
x=1时,y<0,即a+b+c<0,
所以 a+a+c+c<0.
所以 2a+2c<0.
所以 a+c<0.
故错误;
④由图可知,当x=﹣1时,y=0,即a﹣b+c=0.
当x=2时,y>0,即4a+2b+c>0,
所以 4a+2b+b﹣a>0,
所以 3a+3b>0.
所以 a+b>0.
故正确.
故选:D.


科目:初中数学 来源: 题型:
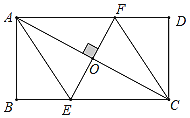
【题目】如图,矩形ABCD的对角线AC的中点为O,过点O作![]() ,交BC边于点E,交AD边于点F,分别连接AE、CF.
,交BC边于点E,交AD边于点F,分别连接AE、CF.
(1)求证:四边形AECF是菱形;
(2)若![]() ,
,![]() ,请直接写出EF的长为__________.
,请直接写出EF的长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙P的圆心P(m,n)在抛物线y=![]() 上.
上.
(1)写出m与n之间的关系式;
(2)当⊙P与两坐标轴都相切时,求出⊙P的半径;
(3)若⊙P的半径是8,且它在x轴上截得的弦MN,满足0≤MN≤2![]() 时,求出m、n的范围.
时,求出m、n的范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
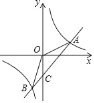
【题目】如图,一次函数y=ax+b(a≠0)的图象与反比例函数y=![]() (k≠0)的图象相交于A、B两点且点A的坐标为(3,1),点B的坐标(﹣1,n).
(k≠0)的图象相交于A、B两点且点A的坐标为(3,1),点B的坐标(﹣1,n).
(1)分别求两个函数的解析式;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某消防队在一居民楼前进行演习,消防员利用云梯成功救出点B处的求救者后,又发现点B正上方点C处还有一名求救者.在消防车上点A处测得点B和点C的仰角分别是45°和65°,点A距地面2.5米,点B距地面10.5米.为救出点C处的求救者,云梯需要继续上升的高度BC约为多少米?(结果保留整数.参考数据:tan65°≈2.1,sin65°≈0.9,cos65°≈0.4,![]() ≈1.4)
≈1.4)

查看答案和解析>>
科目:初中数学 来源: 题型:
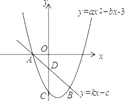
【题目】抛物线y=ax2+bx﹣3(a≠0)与直线y=kx+c(k≠0)相交于A(﹣1,0)、B(2,﹣3)两点,且抛物线与y轴交于点C.
(1)求抛物线的解析式;
(2)求出C、D两点的坐标
(3)在第四象限抛物线上有一点P,若△PCD是以CD为底边的等腰三角形,求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
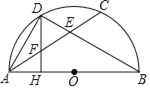
【题目】如图,AB是半圆O的直径,C是半圆上一点,![]() ,DH⊥AB于点H,AC分别交BD、DH于E、F.
,DH⊥AB于点H,AC分别交BD、DH于E、F.
(1)已知AB=10,AD=6,求AH.
(2)求证:DF=EF
查看答案和解析>>
科目:初中数学 来源: 题型:
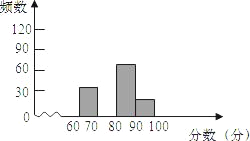
【题目】某校举行手工制作比赛,赛后整理参赛同学的成绩,并制作成图表如下:
分数段 | 频数 | 频率 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | m | 0.45 |
80≤x<90 | 60 | n |
90≤x<100 | 20 | 0.1 |
请根据以上图表提供的信息,解答下列问题:
(1)表中m和n所表示的数分别为:m=______,n=______,
(2)请在图中,补全频数分布直方图;
(3)比赛成绩的中位数落在哪个分数段?
(4)如果比赛成绩80分以上(含80分)可以获得奖励,那么获奖率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
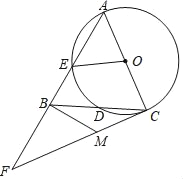
【题目】如图,以△ABC的边AC为直径作⊙O交AB、BC于E、D,D恰为BC的中点,过C作⊙O的切线,与AB的延长线交于F,过B作BM⊥AF,交CF于M.
(1)求证:MB=MC;
(2)若MF=5,MB=3,求⊙O的半径及弦AE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com