
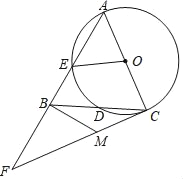
【题目】如图,以△ABC的边AC为直径作⊙O交AB、BC于E、D,D恰为BC的中点,过C作⊙O的切线,与AB的延长线交于F,过B作BM⊥AF,交CF于M.
(1)求证:MB=MC;
(2)若MF=5,MB=3,求⊙O的半径及弦AE的长.
【答案】(1)见解析;(2)EA=![]()
【解析】
(1)连接AD,根据垂直平分线的判定和切线的性质证明即可;
(2)根据相似三角形的判定和性质解答即可.
(1)证明:连接AD,∵AC是⊙O的直径,
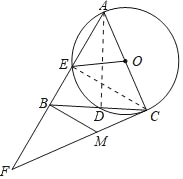
∴∠ADC=90°,
∠ADB=90°,又D是BC的中点,
∴AD是线段BC的垂直平分线,
∴AB=AC,∠ABC=∠ACB,
∵BM⊥AF,CF是⊙O的切线,
∴∠ABM=∠ACM=90°,
∴∠MBC=∠MCB,MB=MC;
(2)∵MF=5,MB=3,
∴FB=4,由上知MC=3,FC=8,
∵∠MBF=∠ACF=90°,∠BFM=∠CFA,
∴△FBM∽△FCA,
∴![]() ,
,
即![]() ,
,
解得:CA=6,⊙O的半径OA=3,
连结CE,则∠AEC=90°,由上知,∠F=∠ACE,则△EAC∽△BMF,
∴![]()
解得:EA=![]()


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过点(﹣1,0),对称轴为直线l,则下列结论:①abc>0;②a+b+c>0;③a+c>0;④a+b>0,正确的是( )

A. ①②④B. ②④C. ①③D. ①④
查看答案和解析>>
科目:初中数学 来源: 题型:
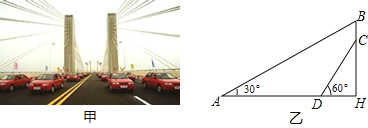
【题目】某大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索顶端的距离BC为2米,两拉索底端距离AD为20米,请求出立柱BH的长.(结果精确到0.1米, ![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
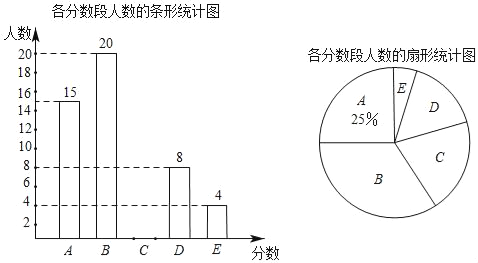
【题目】今年9月28日,某中学初三年级同学进行了中招体育模拟考试,王老师为了更加科学有效地制定后期训练计划,对本班同学的体考成绩进行了统计,并绘制了如图的条形统计图和扇形统计图,其中体育成绩共分为五个等级:A:46分﹣50分;B:41分﹣45分C:36分﹣40分;D:31分﹣35分;E:30分及以下,请根据图中所给的信息完成下列问题:
(1)将上面的条形统计图补充完整:并计算扇形统计图中E等级所对应的圆心角度数为 .
(2)该班A等级中共有5名同学获得满分,其中男同学只有2名,现从这5名同学中任选2名同学在班上进行经验交流,请用树状图或列表法求恰好选到一名男同学和一名女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图抛物线y=ax2+bx+c的对称轴为直线x=1,且过点(3,0),下列结论:①abc>0;②a﹣b+c<0;③2a+b>0;④b2﹣4ac>0;正确的有( )个.
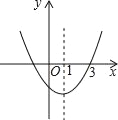
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
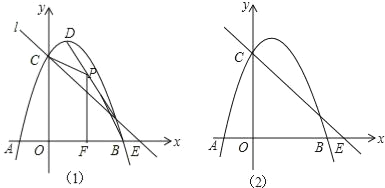
【题目】如图1,抛物线y=﹣x2+2x+3与x轴交于A,B,与y轴交于C,抛物线的顶点为D,直线l过C交x轴于E(4,0).
(1)写出D的坐标和直线l的解析式;
(2)P(x,y)是线段BD上的动点(不与B,D重合),PF⊥x轴于F,设四边形OFPC的面积为S,求S与x之间的函数关系式,并求S的最大值;
(3)点Q在x轴的正半轴上运动,过Q作y轴的平行线,交直线l于M,交抛物线于N,连接CN,将△CMN沿CN翻转,M的对应点为M′.在图2中探究:是否存在点Q,使得M′恰好落在y轴上?若存在,请求出Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
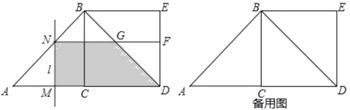
【题目】如图,△ABC中,∠ACB=90°,AC=CB=2,以BC为边向外作正方形BCDE,动点M从A点出发,以每秒1个单位的速度沿着A—C—D的路线向D点匀速运动(M不与A、D重合);过点M作直线l⊥AD,l与路线A—B—D相交于点N,设运动时间为t秒:
(1)当点M在AC上时,BN=_____.(用含t的代数式表示)
(2)过N作NF⊥ED,垂足为F,矩形MDFN与△ABD重叠部分的面积为S,求S的最大值
(3)当点M在CD上时(含点C),是否存在点M,使△DEN为等腰三角形?若存在,直接写出t的值;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市政府规定:若本市企业按生产成本价提供产品给大学生销售,则政府给该企业补偿![]() 补偿额
补偿额![]() 批发价
批发价![]() 生产成本价
生产成本价![]() 销售量
销售量![]() 大学生小明投资销售本市企业生产的一种新型节能灯,调查发现,每月销售量
大学生小明投资销售本市企业生产的一种新型节能灯,调查发现,每月销售量![]() 件
件![]() 与销售单价
与销售单价![]() 元
元![]() 之间的关系近似满足一次函数:
之间的关系近似满足一次函数:![]() 已知这种节能灯批发价为每件12元,设它的生产成本价为每件m元
已知这种节能灯批发价为每件12元,设它的生产成本价为每件m元![]()
(1)当![]() 时.
时.
①若第一个月的销售单价定为20元,则第一个月政府要给该企业补偿多少元?
②设所获得的利润为![]() 元
元![]() ,当销售单价定为多少元时,每月可获得最大利润?
,当销售单价定为多少元时,每月可获得最大利润?
(2)物价部门规定,这种节能灯的销售单价不得超过30元![]() 今年三月小明获得赢利,此时政府给该企业补偿了920元,若m,x都是正整数,求m的值.
今年三月小明获得赢利,此时政府给该企业补偿了920元,若m,x都是正整数,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com