
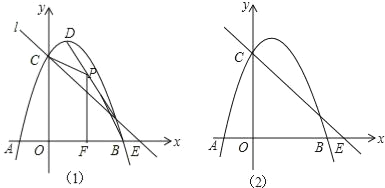
【题目】如图1,抛物线y=﹣x2+2x+3与x轴交于A,B,与y轴交于C,抛物线的顶点为D,直线l过C交x轴于E(4,0).
(1)写出D的坐标和直线l的解析式;
(2)P(x,y)是线段BD上的动点(不与B,D重合),PF⊥x轴于F,设四边形OFPC的面积为S,求S与x之间的函数关系式,并求S的最大值;
(3)点Q在x轴的正半轴上运动,过Q作y轴的平行线,交直线l于M,交抛物线于N,连接CN,将△CMN沿CN翻转,M的对应点为M′.在图2中探究:是否存在点Q,使得M′恰好落在y轴上?若存在,请求出Q的坐标;若不存在,请说明理由.
【答案】(1)y=﹣![]() x+3;(2)
x+3;(2)![]() ;(3)点Q的坐标为(
;(3)点Q的坐标为(![]() ,0)或(4,0).
,0)或(4,0).
【解析】试题(1)先把抛物线解析式配成顶点式即可得到D点坐标,再求出C点坐标,然后利用待定系数法求直线l的解析式;
(2)先根据抛物线与x轴的交点问题求出B(3,0),再利用待定系数法求出直线BD的解析式为y=-2x+6,则P(x,-2x+6),然后根据梯形的面积公式可得S=-x2+![]() x(1≤x≤3),再利用而此函数的性质求S的最大值;
x(1≤x≤3),再利用而此函数的性质求S的最大值;
(3)如图2,设Q(t,0)(t>0),则可表示出M(t,-![]() t+3),N(t,-t2+2t+3),利用两点间的距离公式得到MN=|t2-
t+3),N(t,-t2+2t+3),利用两点间的距离公式得到MN=|t2-![]() t|,CM=
t|,CM=![]() t,然后证明NM=CM得到|t2-
t,然后证明NM=CM得到|t2-![]() t|=
t|=![]() t,再解绝对值方程求满足条件的t的值,从而得到点Q的坐标.
t,再解绝对值方程求满足条件的t的值,从而得到点Q的坐标.
试题解析:(1)∵y=-x2+2x+3=-(x-1)2+4,
∴D(1,4),
当x=0时,y=-x2+2x+3=3,则C(0,3),
设直线l的解析式为y=kx+b,
把C(0,3),E(4,0)分别代入得![]() ,解得
,解得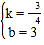 ,
,
∴直线l的解析式为y=-![]() x+3;
x+3;
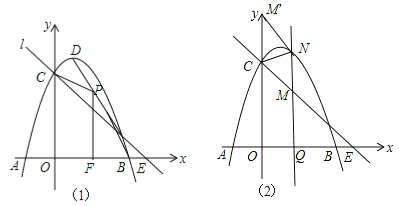
(2)如图(1),当y=0时,-x2+2x+3=0,解得x1=-1,x2=3,则B(3,0),
设直线BD的解析式为y=mx+n,
把B(3,0),D(1,4)分别代入得![]() ,解得
,解得![]() ,
,
∴直线BD的解析式为y=-2x+6,
则P(x,-2x+6),
∴S=![]()
![]() (-2x+6+3)
(-2x+6+3)![]() x=-x2+
x=-x2+![]() x(1≤x≤3),
x(1≤x≤3),
∵S=-(x-![]() )2+
)2+![]() ,
,
∴当x=![]() 时,S有最大值,最大值为
时,S有最大值,最大值为![]() ;
;
(3)存在.
如图2,设Q(t,0)(t>0),则M(t,-![]() t+3),N(t,-t2+2t+3),
t+3),N(t,-t2+2t+3),
∴MN=|-t2+2t+3-(-![]() t+3)|=|t2-
t+3)|=|t2-![]() t|,
t|,
CM=![]() =
=![]() t,
t,
∵△CMN沿CN翻转,M的对应点为M′,M′落在y轴上,
而QN∥y轴,
∴MN∥CM′,NM=NM′,CM′=CM,∠CNM=∠CNM′,
∴∠M′CN=∠CNM,
∴∠M′CN=∠CNM′,
∴CM′=NM′,
∴NM=CM,
∴|t2-![]() t|=
t|=![]() t,
t,
当t2-![]() t=
t=![]() t,解得t1=0(舍去),t2=4,此时Q点坐标为(4,0);
t,解得t1=0(舍去),t2=4,此时Q点坐标为(4,0);
当t2-![]() t=-
t=-![]() t,解得t1=0(舍去),t2=
t,解得t1=0(舍去),t2=![]() ,此时Q点坐标为(
,此时Q点坐标为(![]() ,0),
,0),
综上所述,点Q的坐标为(![]() ,0)或(4,0).
,0)或(4,0).


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】为推动全面健身,县政府在城南新城新建体育休闲公园,公园设有A、B、C、D四个出入口供广大市民进出.
(1)小明的爸爸去公园进行体育锻炼,从出入口A进入的概率是________;
(2)张老师和小明的爸爸一起约定去参加锻炼,请用画树状图或列表法求他们选择从不同出入口进体育场的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,![]() 是直角,
是直角,![]() 在
在![]() 的外侧,且
的外侧,且![]() ,
,![]() 是
是![]() 的平分线,
的平分线,![]() 是
是![]() 的平分线.
的平分线.
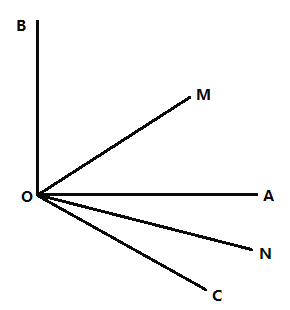
(1)求![]() 的大小;
的大小;
(2)当锐角![]() 的大小为
的大小为![]() 时,试猜想(1)中
时,试猜想(1)中![]() 的大小是否发生改变?并通过计算说明理由.
的大小是否发生改变?并通过计算说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
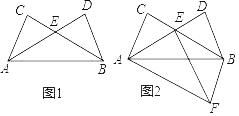
【题目】如图1,点C、D是线段AB同侧两点,且AC=BD,∠CAB=∠DBA,连接BC,AD交于点 E.
(1)求证:AE=BE;
(2)如图2,△ABF与△ABD关于直线AB对称,连接EF.
①判断四边形ACBF的形状,并说明理由;
②若∠DAB=30°,AE=5,DE=3,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
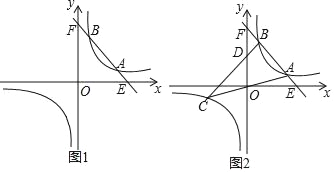
【题目】已知:一次函数y=﹣2x+10的图象与反比例函数y=![]() (k>0)的图象相交于A、B两点(A的B的右侧).
(k>0)的图象相交于A、B两点(A的B的右侧).
(1)当A(4,2)时,求反比例函数的解析式:
(2)当A的横坐标是3,B的横坐标是2时,直线OA与此反比例函数图象的另一支交于另一点C,连接BC交y轴于点D.
①求C点的坐标;
②求D点的坐标;
③求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
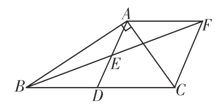
【题目】如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)求证:四边形ADCF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司购买了一批A、B两种型号的产品,其中A型产品的单价比B型产品的单价多6元,已知该公司用1400元购买A型产品的件数与用1160元购买B型产品的件数相等.
(1)求该公司购买的A、B两种型号产品的单价各是多少元?
(2)若两种型号的产品共购买了100件,且购买的总费用为3260元,求购买了多少件A型产品?
查看答案和解析>>
科目:初中数学 来源: 题型:
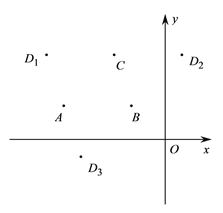
【题目】在平面直角坐标系![]() 中,已知点
中,已知点![]() ,
,![]() ,
,![]() ,其中
,其中![]() ,以点
,以点![]() 为顶点的平行四边形有三个,记第四个顶点分别为
为顶点的平行四边形有三个,记第四个顶点分别为![]() ,如图所示.
,如图所示.
(1)若![]() ,则点
,则点![]() 的坐标分别是( ),( ),( );
的坐标分别是( ),( ),( );
(2)是否存在点![]() ,使得点
,使得点![]() 在同一条抛物线上?若存在,求出点
在同一条抛物线上?若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生会为积极响应武汉市文明创建活动,组织有关方面的知识竞赛,共设有20道选择题,各题分值相同,每题必答,下表记录了3个参赛者的得分情况.
参赛者 | 答对题数 | 答错题数 | 得分 |
A | 20 | 0 | 100 |
B | 19 | 1 | 94 |
C | 18 | 2 | 88 |
(1)设答对一题记a分,答错一题记b分,则a= b= ;
(2)参赛者E说他得了80分,你认为可能吗,为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com