
【题目】已知:如图,![]() 是直角,
是直角,![]() 在
在![]() 的外侧,且
的外侧,且![]() ,
,![]() 是
是![]() 的平分线,
的平分线,![]() 是
是![]() 的平分线.
的平分线.
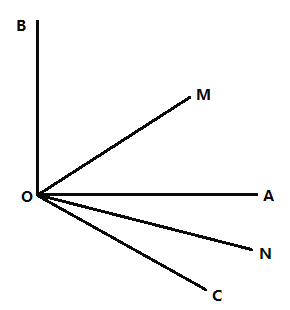
(1)求![]() 的大小;
的大小;
(2)当锐角![]() 的大小为
的大小为![]() 时,试猜想(1)中
时,试猜想(1)中![]() 的大小是否发生改变?并通过计算说明理由.
的大小是否发生改变?并通过计算说明理由.
【答案】(1)45°;(2)∠MON的大小不发生改变,即∠MON=45°,理由见解析.
【解析】
(1)根据∠AOB是直角,∠AOC=40°,可得∠AOB+∠AOC=90°+40°=130°,再利用OM是∠BOC的平分线,ON是∠AOC的平分线,即可求得答案.
(2)根据∠BOC=∠AOB+∠AOC=90°+![]() ,∠MON=∠MOC-∠NOC,可得∠MON=
,∠MON=∠MOC-∠NOC,可得∠MON=![]() ∠AOB=45°.
∠AOB=45°.
(1)∵∠AOB是直角,∠AOC=40°.
∴∠BOC=∠AOB+∠AOC=90°+40°=130°
∵ON是∠AOC的平分线,OM是∠BOC的平分线
∴∠COM=![]() ∠BOC=
∠BOC=![]() ×130°=65°,∠CON=
×130°=65°,∠CON=![]() ∠AOC=
∠AOC=![]() ×40°=20°,
×40°=20°,
∴∠MON=∠COM-∠CON=65°-20°=45°
(2)当锐角∠AOC的大小为![]() 时,∠MON的大小不发生改变,即∠MON=45°
时,∠MON的大小不发生改变,即∠MON=45°
理由:当∠AOC=![]() 时,∠BOC=∠AOB+∠AOC=90°+
时,∠BOC=∠AOB+∠AOC=90°+![]()
∵ON是∠AOC的平分线,OM是∠BOC的平分线
∴∠COM=![]() ∠BOC=
∠BOC=![]() ×(90°+
×(90°+![]() )=45°+
)=45°+![]()
![]() ,∠CON=
,∠CON=![]() ∠AOC=
∠AOC=![]()
![]() ,
,
∴∠MON=∠COM-∠CON=45°+![]()
![]() -
-![]()
![]() =45°
=45°


 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】问题情境
在综合与实践课上,老师让同学们以“两条平行线AB,CD和一块含60°角的直角三角尺EFG(∠EFG=90°,∠EGF=60°)”为主题开展数学活动.
操作发现
(1)如图(1),小明把三角尺的60°角的顶点G放在CD上,若∠2=2∠1,求∠1的度数;
(2)如图(2),小颖把三角尺的两个锐角的顶点E、G分别放在AB和CD上,请你探索并说明∠AEF与∠FGC之间的数量关系;
结论应用
(3)如图(3),小亮把三角尺的直角顶点F放在CD上,30°角的顶点E落在AB上.若∠AEG=α,则∠CFG等于______(用含α的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某市2018年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图.
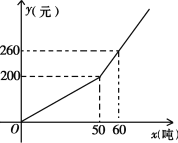
(1)当x≥50时,求y关于x的函数关系式;
(2)若某企业2018年10月份的水费为620元,求该企业2018年10月份的用水量.
查看答案和解析>>
科目:初中数学 来源: 题型:
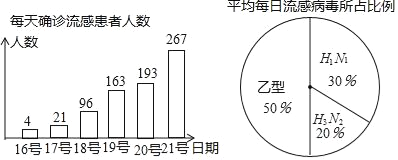
【题目】2017年12月,乙型,甲型H3N2和甲型H1N1三种禽流感病毒共同发威,造成流感在某市迅速蔓延,下面是该市确诊流感患者的统计图:
(1)在12月18日,该市被确诊的流感患者中多少乙型流感患者?
(2)在12月17日至21日这5天中,该市平均每天新增流感确诊病例多少人?如果接下来的5天中继续按这个平均数增加,那么到12月26日,该市流感累计确诊病例将会达到多少人?
(3)某地因1人患了流感没有及时隔离治疗,经过两天传染后共有9人患了流感,每天传染中平均一个人传染了几个人?
查看答案和解析>>
科目:初中数学 来源: 题型:
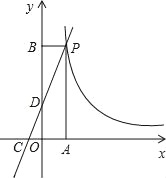
【题目】如图,一次函数y=kx+2的图象与反比例函数y=![]() 的图象在第一象限的交点为P,PA⊥x轴于点A,PB⊥y轴于点B,函数y=kx+2的图象分别交x轴,y轴于点C,D,已知△OCD的面积S△OCD=1,
的图象在第一象限的交点为P,PA⊥x轴于点A,PB⊥y轴于点B,函数y=kx+2的图象分别交x轴,y轴于点C,D,已知△OCD的面积S△OCD=1,![]() =
=![]()
(1)求点D的坐标;
(2)求k,m的值;
(3)写出当x>0时,使一次函数y=kx+2的值大于反比例函数y=![]() 的值x的取值范围.
的值x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在菱形ABCD中,AB=2,∠BAD=60°,过点D作DE⊥AB点E,DF⊥BC于点F.将∠EDF绕点D顺时针旋转α°(0<α<180),其两边的对应边DE′、DF′分别与直线AB、BC相交于点G、P,如图2.连接GP,当△DGP的面积等于3![]() 时,则α的大小为( )
时,则α的大小为( )
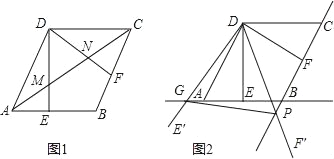
A. 30 B. 45 C. 60 D. 120
查看答案和解析>>
科目:初中数学 来源: 题型:
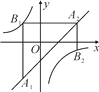
【题目】如图,已知点A1,A2,…,An均在直线y=x-1上,点B1,B2,…,Bn均在双曲线y=-![]() 上,并且满足A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=-1,则a2018=_______.
上,并且满足A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=-1,则a2018=_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
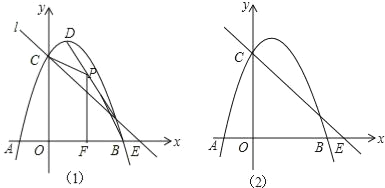
【题目】如图1,抛物线y=﹣x2+2x+3与x轴交于A,B,与y轴交于C,抛物线的顶点为D,直线l过C交x轴于E(4,0).
(1)写出D的坐标和直线l的解析式;
(2)P(x,y)是线段BD上的动点(不与B,D重合),PF⊥x轴于F,设四边形OFPC的面积为S,求S与x之间的函数关系式,并求S的最大值;
(3)点Q在x轴的正半轴上运动,过Q作y轴的平行线,交直线l于M,交抛物线于N,连接CN,将△CMN沿CN翻转,M的对应点为M′.在图2中探究:是否存在点Q,使得M′恰好落在y轴上?若存在,请求出Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,P为对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F,连接CE.
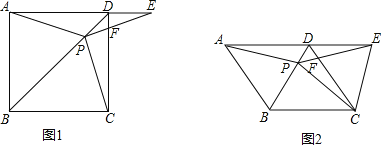
(1)求证:△PCE是等腰直角三角形;
(2)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,判断△PCE的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com