
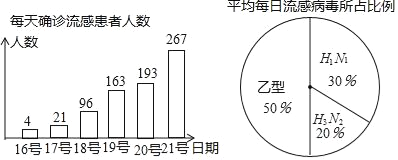
����Ŀ��2017��12�£����ͣ�����H3N2�ͼ���H1N1���������в�����ͬ���������������ij��Ѹ�����ӣ������Ǹ���ȷ�����л��ߵ�ͳ��ͼ��
��1����12��18�գ����б�ȷ������л����ж����������л��ߣ�
��2����12��17����21����5���У�����ƽ��ÿ����������ȷ�ﲡ�������ˣ������������5���м��������ƽ�������ӣ���ô��12��26�գ����������ۼ�ȷ�ﲡ������ﵽ�����ˣ�
��3��ij����1�˻�������û�м�ʱ�������ƣ��������촫Ⱦ����9�˻������У�ÿ�촫Ⱦ��ƽ��һ���˴�Ⱦ�˼����ˣ�
���𰸡�(1) 48�ˣ� ��2��52.6�ˣ� 530�ˣ� ��3��2����.
��������
��1������ͳ��ͼ�е���Ϣ��֪��12��18�չ���96��ȷ��Ϊ���л��ߣ�������������ռ��Ϊ50%���ɴ˼��ɼ��������ȷ��Ϊ�������л��ߵ�������
��2����������ͳ��ͼ�е���Ϣ��ʽ���㼴�ɣ�
��3����ƽ��ÿ��һ�����ߴ�Ⱦx���ˣ����������г����̣��ⷽ�̼�������������.
��1������ͳ��ͼ�е���Ϣ�ɵã�96��50%=48���ˣ�
����12��18�գ����б�ȷ������л�����48�����������л��ߣ�
��2��������ɵ���
12��17����12��21����5������ƽ��ÿ����������ȷ�ﻼ������Ϊ��
��267��4����5=52.6��
��������5����������ƽ�������ӣ���12��26���������е��ۼ�ȷ�ﲡ�����
167+52.6��5=530���ˣ�.
����12��17����12��21����5���У�����ƽ��ÿ����������ȷ�ﲡ��52.6�ˣ���12��26�ո��������ۼ�ȷ�ﲡ������ﵽ530�ˣ�
��3����ƽ��һ����һ�촫Ⱦx���ˣ���������ɵã�
x��x+1��+x+1=9
x=2��x=��4����ȥ����
��ÿ�촫Ⱦ��ƽ��һ���˴�Ⱦ��2���ˣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ijѧУ����֯ѧ����ѧ���ҳ����Ͼ���ѧ�ι����飬Ϊ�˱��ڹ�����������Ա���Ͼ����������ͬһ�ж����ϣ����ݱ���������������һ�������̻�Ʊ��5032Ԫ����������������̻�Ʊ�һ�Ǯ���٣�����2970Ԫ����֪ѧ���ҳ������ǽ�ʦ������2�����������Ͼ��Ķ���Ʊ�۸���ѧ��Ʊֻ�ж��������Դ�6�ۣ����±���ʾ��
�������� | Ʊ�� | ||
�ϳ�վ | �³�վ | һ���� | ������ |
���� | �Ͼ� | 68��Ԫ�� | 55��Ԫ�� |
��1���μӲι��������ʦ���ҳ���ѧ�����ж����ˣ�
��2�����ڸ���ԭ��������Ʊ����ֻ����x�ţ�xС�ڲμ�����������������������һ������Ʊ���ڱ�֤ÿλ������Ա������λ����ǰ���£����������õĹ�Ʊ��������д�������Ʊ���ܷ��ã����̣�y��x֮��ĺ�����ϵʽ��
��3��������һ��Ԥ�㣬���ڣ�2��С���еĹ�Ʊ���������̻�Ʊ���ܷ��������Ƕ���Ǯ������Ƕ���Ǯ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�ƶ�ȫ�潡�����������ڳ����³��½��������й���������A��B��C��D�ĸ�����ڹ�������������
��1��С���İְ�ȥ�����������������ӳ����A����ĸ�����________��
��2������ʦ��С���İְ�һ��Լ��ȥ�μӶ��������û���״ͼ���б���������ѡ��Ӳ�ͬ����ڽ��������ĸ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() ��
��![]() �ֱ���ֱ��
�ֱ���ֱ��![]() ��
��![]() �ϣ���
�ϣ���![]() ��ֱ��
��ֱ��![]() ��
��![]() ֮�䣬
֮�䣬![]() ��
��
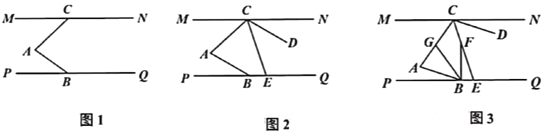
��1����ͼ1����֤��![]() ��
��
��2����ͼ2������![]() ��
��![]() ����
����![]() ��
��![]() �ϣ�
�ϣ�![]() ����֤��
����֤��![]() ��
��
��3���ڣ�2���������£���ͼ3������![]() ��
��![]() �Ĵ��߽�
�Ĵ��߽�![]() �ڵ�
�ڵ�![]() ��
��![]() ��ƽ���߽�
��ƽ���߽�![]() �ڵ�
�ڵ�![]() ����
����![]() ��
��![]() ����
����![]() �Ķ�����
�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABC�У���A=90�㣬AB=AC=2������ABC�۵���ʹ��B���ڱ�AC�ϵ�D �������A�غϣ������ۺ�ΪPQ�����ص�������PQDΪ����������ʱ����AD�ij�Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�͡�ADE�У�AB=AC��AD=AE���ҡ�BAC=��DAE����E��BC�ϣ�����D��DF��BC������DB��

��֤����1����ABD�ա�ACE��
��2��DF=CE��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��![]() ��ֱ�ǣ�
��ֱ�ǣ�![]() ��
��![]() ����࣬��
����࣬��![]() ��
��![]() ��
��![]() ��ƽ���ߣ�
��ƽ���ߣ�![]() ��
��![]() ��ƽ���ߣ�
��ƽ���ߣ�
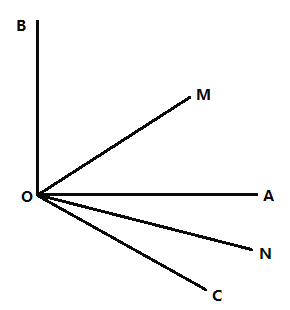
��1����![]() �Ĵ�С��
�Ĵ�С��
��2�������![]() �Ĵ�СΪ
�Ĵ�СΪ![]() ʱ���Բ��루1����
ʱ���Բ��루1����![]() �Ĵ�С�Ƿ����ı䣿��ͨ������˵�����ɣ�
�Ĵ�С�Ƿ����ı䣿��ͨ������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
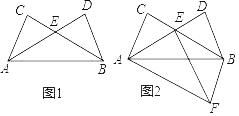
����Ŀ����ͼ1����C��D���߶�ABͬ�����㣬��AC��BD����CAB����DBA������BC��AD���ڵ� E��
��1����֤��AE��BE��
��2����ͼ2����ABF���ABD����ֱ��AB�Գƣ�����EF��
���ж��ı���ACBF����״����˵�����ɣ�
������DAB��30�㣬AE��5��DE��3�����߶�EF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
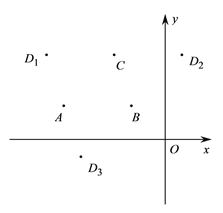
����Ŀ����ƽ��ֱ������ϵ![]() �У���֪��
�У���֪��![]() ��
��![]() ��
��![]() ������
������![]() ���Ե�
���Ե�![]() Ϊ�����ƽ���ı������������ǵ��ĸ�����ֱ�Ϊ
Ϊ�����ƽ���ı������������ǵ��ĸ�����ֱ�Ϊ![]() ����ͼ��ʾ.
����ͼ��ʾ.
��1����![]() �����
�����![]() ������ֱ��ǣ� ������ ������ ����
������ֱ��ǣ� ������ ������ ����
��2���Ƿ���ڵ�![]() ��ʹ�õ�
��ʹ�õ�![]() ��ͬһ���������ϣ������ڣ������
��ͬһ���������ϣ������ڣ������![]() �����ꣻ�������ڣ�˵������.
�����ꣻ�������ڣ�˵������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com