
【题目】无锡某学校准备组织学生及学生家长到南京大学参观体验,为了便于管理,所有人员到南京必须乘坐在同一列动车上;根据报名人数,若都买一等座单程火车票需5032元,若都买二等座单程火车票且花钱最少,则需2970元;已知学生家长人数是教师人数的2倍,无锡到南京的动车票价格(动车学生票只有二等座可以打6折)如下表所示:
运行区间 | 票价 | ||
上车站 | 下车站 | 一等座 | 二等座 |
无锡 | 南京 | 68(元) | 55(元) |
(1)参加参观体验的老师、家长与学生各有多少人?
(2)由于各种原因,二等座火车票单程只能买x张(x小于参加体验的人数),其余的需买一等座火车票,在保证每位参与人员都有座位坐的前提下,请你设计最经济的购票方案,并写出购买火车票的总费用(单程)y与x之间的函数关系式.
(3)请你做一个预算,按第(2)小题中的购票方案,购买单程火车票的总费用至少是多少钱?最多是多少钱?
【答案】(1)参加参观体验的老师有8人,家长有16人,学生有50人(2)y=![]() (3)购买单程火车票的总费用至少是2983元,最多是5032元
(3)购买单程火车票的总费用至少是2983元,最多是5032元
【解析】分析: (1)设参加社会实践的老师有m人,学生有n人,则学生家长有2m人,若都买二等座单程火车票且花钱最少,则全体学生都需买二等座学生票,根据题意得到方程组:![]() ,求出方程组的解即可;
,求出方程组的解即可;
(2)有两种情况:①当0≤x<50时,学生都买学生票共50张,(x-50)名成年人买二等座火车票,(74-x)名成年人买一等座火车票,得到解析式:y=55×0.6x+68×(74﹣x)=﹣34x+5032,②当50≤x<74时,一部分学生买学生票共x张,其余的学生与家长老师一起购买一等座火车票共(74-x)张,得到解析式是y=55×0.6×50+55×(x﹣50)+68×(74﹣x)=﹣13x+3932;
(3)由(2)小题知,当0≤x<50时,y=﹣34x+5032和当50≤x<74时,y=﹣13x+3932,分别讨论即可.
详解:
(1)设参加参观体验的老师有m人、学生有n人,则家长有2m人,根据已知得:
![]() , 解得:
, 解得:![]() .
.
2m=2×8=16.
答:参加参观体验的老师有8人,家长有16人,学生有50人.
(2)由(1)可知报名参观体验的总人数为8+16+50=74(人).
二等车票只能购买x张,则一等车票购买了74﹣x张.
当0≤x<50时,y=55×0.6x+68×(74﹣x)=﹣34x+5032;
当50≤x<74时,y=55×0.6×50+55×(x﹣50)+68×(74﹣x)=﹣13x+3932.
故购买火车票的总费用(单程)y与x之间的函数关系式为y=![]() .
.
(3)由(2)的函数关系式可知:
当x=0时,y最高,此时y=5032;
当x=73时,y最小,此时y=2983.
答:购买单程火车票的总费用至少是2983元,最多是5032元.
点睛: 本题主要考查对一次函数,二元一次方程组,一元一次不等式等知识,解题的关键是理解题意,学会构建方程组或一次函数解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:
【题目】如图1,在平行四边形![]() 中,点
中,点![]() 是对角线
是对角线![]() 的中点,
的中点,![]() 过点
过点![]() 与
与![]() ,
,![]() 分别相交于
分别相交于![]() ,
,![]() ,
,![]() 过点
过点![]() 与
与![]() ,
,![]() 分别相交于点
分别相交于点![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)如图2,若![]() ,
,![]() ,在不添加任何辅助的情况下,请直接写出图2中与四边形
,在不添加任何辅助的情况下,请直接写出图2中与四边形![]() 面积相等的所有的平行四边形(四边形
面积相等的所有的平行四边形(四边形![]() 除外).
除外).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(1,2)为反比例函数![]() 图象上一点,
图象上一点,
(1) 将点A沿x轴正方向平移1个单位,对应点A′的坐标为___________
将比例函数![]() 图象沿x轴正方向平移1个单位,平移后的函数解析式为___________
图象沿x轴正方向平移1个单位,平移后的函数解析式为___________
将比例函数![]() 图象沿x轴正方向平移m个单位,平移后的函数解析式为___________
图象沿x轴正方向平移m个单位,平移后的函数解析式为___________
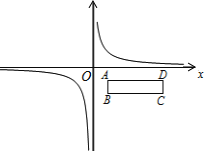
(2) 在平面直角坐标系中,矩形ABCD位置如图,其中A、B、C三点的坐标分别为A(1,-1)、B(1,-2)、C(4,-2).现将反比例函数![]() 图象沿x轴正方向平移,若平移速度为每秒1个单位长度
图象沿x轴正方向平移,若平移速度为每秒1个单位长度
① 设函数图象平移时间为t秒,求函数图象与矩形ABCD有公共点时t的取值范围;
② 在平移过程中,当函数图象与矩形ABCD有公共点时,则函数图象扫过的区域夹在直线AD、BC的图形面积为___________(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】食品厂从生产的袋装食品中抽出样品![]() 袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正、负来表示,记录如下表;
袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正、负来表示,记录如下表;
与标准质量的差值(单位:克) |
|
|
|
|
|
|
袋数 |
|
|
|
|
|
|
(1)这批样品的平均质量比标准质量是超过还是不足?平均每袋超过或不足多少克?
(2)若每袋标准质量为![]() 克,求抽样检测的样品总质量是多少?
克,求抽样检测的样品总质量是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=8,BC=6.CD⊥AB于点D.点P从点A出发,以每秒1个单位长度的速度沿线段AB向终点B运动.在运动过程中,以点P为顶点作长为2,宽为1的矩形PQMN,其中PQ=2,PN=1,点Q在点P的左侧,MN在PQ的下分,且PQ总保持与AC垂直.设P的运动时间为t(秒)(t>0),矩形PQMN与△ACD的重叠部分图形面积为S(平方单位).
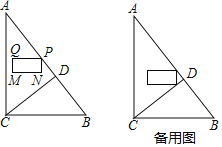
(1)求线段CD的长;
(2)当矩形PQMN与线段CD有公共点时,求t的取值范围;
(3)当点P在线段AD上运动时,求S与t的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给下列证明过程填写理由.
如图,CD⊥AB于D,点F是BC上任意一点,EF⊥AB于E,∠1=∠2,求证:∠ACB=∠3.
请阅读下面解答过程,并补全所有内容.
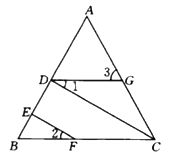
解:∵CD⊥AB,EF⊥AB(已知)
∴∠BEF=∠BDC=90°( )
∴EF∥DC( )
∴∠2=________( )
又∵∠2=∠1(已知)
∴∠1=_______(等量代换)
∴DG∥BC( )
∴∠3=________( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境
在综合与实践课上,老师让同学们以“两条平行线AB,CD和一块含60°角的直角三角尺EFG(∠EFG=90°,∠EGF=60°)”为主题开展数学活动.
操作发现
(1)如图(1),小明把三角尺的60°角的顶点G放在CD上,若∠2=2∠1,求∠1的度数;
(2)如图(2),小颖把三角尺的两个锐角的顶点E、G分别放在AB和CD上,请你探索并说明∠AEF与∠FGC之间的数量关系;
结论应用
(3)如图(3),小亮把三角尺的直角顶点F放在CD上,30°角的顶点E落在AB上.若∠AEG=α,则∠CFG等于______(用含α的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知坐标平面内的三个点![]() ,
,![]() ,
,![]() ,把
,把![]() 向下平移
向下平移![]() 个单位再向右平移
个单位再向右平移![]() 个单位后得到
个单位后得到![]() .
.
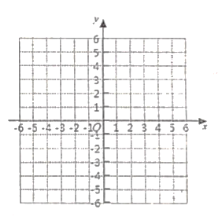
(1)直接写出![]() ,
,![]() ,
,![]() 三个对应点
三个对应点![]() 、
、![]() 、
、![]() 的坐标;
的坐标;
(2)画出将![]() 绕
绕![]() 点逆时针方向旋转
点逆时针方向旋转![]() 后得到
后得到![]() ;
;
(3)求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
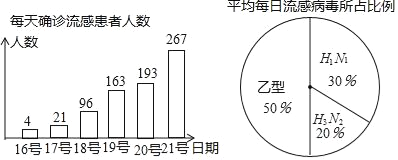
【题目】2017年12月,乙型,甲型H3N2和甲型H1N1三种禽流感病毒共同发威,造成流感在某市迅速蔓延,下面是该市确诊流感患者的统计图:
(1)在12月18日,该市被确诊的流感患者中多少乙型流感患者?
(2)在12月17日至21日这5天中,该市平均每天新增流感确诊病例多少人?如果接下来的5天中继续按这个平均数增加,那么到12月26日,该市流感累计确诊病例将会达到多少人?
(3)某地因1人患了流感没有及时隔离治疗,经过两天传染后共有9人患了流感,每天传染中平均一个人传染了几个人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com