
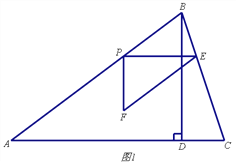
【题目】如图,在△ABC中,∠ACB=90°,AC=8,BC=6.CD⊥AB于点D.点P从点A出发,以每秒1个单位长度的速度沿线段AB向终点B运动.在运动过程中,以点P为顶点作长为2,宽为1的矩形PQMN,其中PQ=2,PN=1,点Q在点P的左侧,MN在PQ的下分,且PQ总保持与AC垂直.设P的运动时间为t(秒)(t>0),矩形PQMN与△ACD的重叠部分图形面积为S(平方单位).
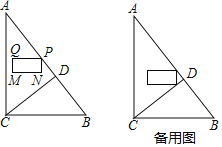
(1)求线段CD的长;
(2)当矩形PQMN与线段CD有公共点时,求t的取值范围;
(3)当点P在线段AD上运动时,求S与t的函数关系式.
【答案】(1)CD=![]() ;(2)
;(2)![]() ≤t≤
≤t≤![]() ;(3)当0<t<
;(3)当0<t<![]() 时,S=
时,S=![]() ;当
;当![]() ≤t≤
≤t≤![]() 时, S=2;当
时, S=2;当![]() <t≤
<t≤![]() 时,S=
时,S=![]() .
.
【解析】
(1)由勾股定理得出AB=10,由△ABC的面积得出ACBC=ABCD,即可得出CD的长;
(2)分两种情形:①当点N在线段CD上时,如图1所示,利用相似三角形的性质求解即可.②当点Q在线段CD上时,如图2所示,利用相似三角形的性质求解即可;
(3)首先求出点Q落在AC上的运动时间t,再分三种情形:①当0<t<![]() 时,重叠部分是矩形PNYH,如图4所示,②当
时,重叠部分是矩形PNYH,如图4所示,②当![]() ≤t≤
≤t≤![]() 时,重合部分是矩形PNMQ,S=PQPN=2,③当
时,重合部分是矩形PNMQ,S=PQPN=2,③当![]() <t≤
<t≤![]() 时,如图5中重叠部分是五边形PQMJI,分别求解即可.
时,如图5中重叠部分是五边形PQMJI,分别求解即可.
解:(1)∵∠ACB=90°,AC=8,BC=6,
∴AB=![]() =10,
=10,
∵S△ABC=![]() ACBC=
ACBC=![]() ABCD,
ABCD,
∴ACBC=ABCD,即:8×6=10×CD,
∴CD=![]() ;
;
(2)在Rt△ADC中,AD=![]() ,BD=ABAD=
,BD=ABAD=![]() ,
,
当点N在线段CD上时,如图1所示:
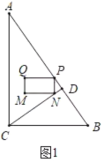
∵矩形PQMN,PQ总保持与AC垂直,
∴PN∥AC,
∴∠NPD=∠CAD,
∵∠PDN=∠ADC,
∴△PDN∽△ADC,
∴![]() ,即:
,即: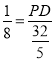 ,
,
解得:PD=![]() ,
,
∴t=ADPD=![]() ;
;
当点Q在线段CD上时,如图2所示:

∵PQ总保持与AC垂直,
∴PQ∥BC,△DPQ∽△DBC,
∴![]() ,即:
,即: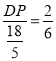 ,
,
解得:DP=![]() ,
,
∴t=AD+DP=![]() ,
,
∴当矩形PQMN与线段CD有公共点时,t的取值范围为:![]() ≤t≤
≤t≤![]() ;
;
(3)当Q在AC上时,如图3所示:
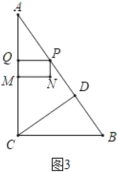
∵PQ总保持与AC垂直,
∴PQ∥BC,△APQ∽△ABC,
∴![]() ,即:
,即:![]() ,
,
解得:AP=![]() ,
,
当0<t<![]() 时,重叠部分是矩形PNYH,如图4所示:
时,重叠部分是矩形PNYH,如图4所示:
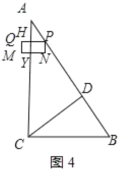
∵PQ∥BC,
∴△APH∽△ABC,
∴![]() ,即:
,即:![]() ,
,
∴PH=![]() ,
,
∴S=PHPN=![]() ;
;
当![]() ≤t≤
≤t≤![]() 时,重合部分是矩形PNMQ,S=PQPN=2;
时,重合部分是矩形PNMQ,S=PQPN=2;
当![]() <t≤
<t≤![]() 时,如图5中重叠部分是五边形PQMJI,
时,如图5中重叠部分是五边形PQMJI,
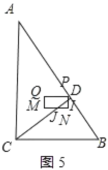
易得△PDI∽△ACB∽△JNI,
∴![]() ,即:
,即: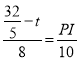 ,
,
∴PI=(![]() t)
t)![]() ,
,
∴![]() ,即:
,即: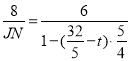 ,
,
∴JN=![]() ,
,
S=S矩形PNMQS△JIN=2![]() ·(
·(![]() )·[1(
)·[1(![]() t)
t)![]() ]=
]=![]() .
.


科目:初中数学 来源: 题型:
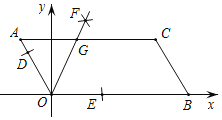
【题目】如图,已知AOBC的顶点O(0,0),A(﹣1,2),点B在x轴正半轴上按以下步骤作图:①以点O为圆心,适当长度为半径作弧,分别交边OA,OB于点D,E;②分别以点D,E为圆心,大于![]() DE的长为半径作弧,两弧在∠AOB内交于点F;③作射线OF,交边AC于点G,则点G的坐标为( )
DE的长为半径作弧,两弧在∠AOB内交于点F;③作射线OF,交边AC于点G,则点G的坐标为( )
A. (![]() ﹣1,2) B. (
﹣1,2) B. (![]() ,2) C. (3﹣
,2) C. (3﹣![]() ,2) D. (
,2) D. (![]() ﹣2,2)
﹣2,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个水果市场某品种苹果的销售方式如下表:
购买苹数量(千克) | 不超过 | 超过 |
每千克的价格(元) |
|
|
(1)如果小明购买![]() 千克的苹果,那么他需要付___________元.
千克的苹果,那么他需要付___________元.
(2)小明分两次共购买![]() 千克的苹果,第二次购买的数量多于第一次购买的数量,若他两次共付
千克的苹果,第二次购买的数量多于第一次购买的数量,若他两次共付![]() 元,求他两次分别购买苹果的数量.
元,求他两次分别购买苹果的数量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着粤港澳大湾区建设的加速推进,广东省正加速布局以5G等为代表的战略性新兴产业,据统计,目前广东5G基站的数量约1.5万座,计划到2020年底,全省5G基站数是目前的4倍,到2022年底,全省5G基站数量将达到17.34万座。
(1)计划到2020年底,全省5G基站的数量是多少万座?;
(2)按照计划,求2020年底到2022年底,全省5G基站数量的年平均增长率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点![]() 为直线
为直线![]() 上一点,过点
上一点,过点![]() 作射线
作射线![]() ,使
,使![]() 将一直角三角板的直角顶点放在点
将一直角三角板的直角顶点放在点![]() 处,一边
处,一边![]() 在射线
在射线![]() 上,另一边
上,另一边![]() 在直线
在直线![]() 的下方.
的下方.
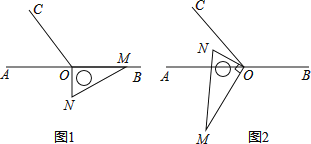
(1)将图1中的三角板绕点![]() 按每秒
按每秒![]() 的速度沿顺时针方向旋转,使
的速度沿顺时针方向旋转,使![]() 落在
落在![]() 上.在旋转的过程中,假如第
上.在旋转的过程中,假如第![]() 秒时,
秒时,![]() 、
、![]() 、
、![]() 三条射线构成的角中有两个角相等,求此时
三条射线构成的角中有两个角相等,求此时![]() 的值为多少?
的值为多少?
(2)将图1中的三角板绕点![]() 顺时针旋转(如图2),使
顺时针旋转(如图2),使![]() 在
在![]() 的内部,请探究:
的内部,请探究:![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】无锡某学校准备组织学生及学生家长到南京大学参观体验,为了便于管理,所有人员到南京必须乘坐在同一列动车上;根据报名人数,若都买一等座单程火车票需5032元,若都买二等座单程火车票且花钱最少,则需2970元;已知学生家长人数是教师人数的2倍,无锡到南京的动车票价格(动车学生票只有二等座可以打6折)如下表所示:
运行区间 | 票价 | ||
上车站 | 下车站 | 一等座 | 二等座 |
无锡 | 南京 | 68(元) | 55(元) |
(1)参加参观体验的老师、家长与学生各有多少人?
(2)由于各种原因,二等座火车票单程只能买x张(x小于参加体验的人数),其余的需买一等座火车票,在保证每位参与人员都有座位坐的前提下,请你设计最经济的购票方案,并写出购买火车票的总费用(单程)y与x之间的函数关系式.
(3)请你做一个预算,按第(2)小题中的购票方案,购买单程火车票的总费用至少是多少钱?最多是多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
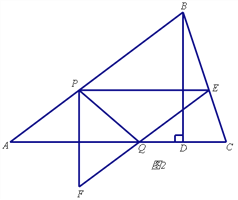
【题目】如图1,在锐角△ABC中,AB=5,tanC=3,BD⊥AC于点D,BD=3,点P从点A出发,以每秒1个单位长度的速度沿AB向终点B运动,过点P作PE∥AC交边BC于点E,以PE为边作Rt△PEF,使∠EPF=90°,点F在点P的下方,且EF∥AB.设△PEF与△ABD重叠部分图形的面积为S(平方单位)(S>0),点P的运动时间为t(秒)
(t>0).
(1)求线段AC的长.
(2)当△PEF与△ABD重叠部分图形为四边形时,求S与t之间的函数关系式,并写出t的取值范围.
(3)若边EF所在直线与边AC交于点Q,连结PQ,如图2,直接写出△ABC的某一顶点到P、Q两点距离相等时t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在三角形ABC中,∠A=90°,AB=AC=2,将△ABC折叠,使点B落在边AC上点D (不与点A重合)处,折痕为PQ,当重叠部分△PQD为等腰三角形时,则AD的长为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com