
【题目】一个水果市场某品种苹果的销售方式如下表:
购买苹数量(千克) | 不超过 | 超过 |
每千克的价格(元) |
|
|
(1)如果小明购买![]() 千克的苹果,那么他需要付___________元.
千克的苹果,那么他需要付___________元.
(2)小明分两次共购买![]() 千克的苹果,第二次购买的数量多于第一次购买的数量,若他两次共付
千克的苹果,第二次购买的数量多于第一次购买的数量,若他两次共付![]() 元,求他两次分别购买苹果的数量.
元,求他两次分别购买苹果的数量.
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,以点A为圆心,AC为半径,作⊙A交AB于点D,交CA的延长线于点E,过点E作AB的平行线EF交⊙A于点F,连接AF、BF、DF
(1)求证:BF是⊙A的切线.
(2)当∠CAB等于多少度时,四边形ADFE为菱形?请给予证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知![]() ,对应的坐标如下,请利用学过的变换(平移、旋转、轴对称)知识经过若干次图形变化,使得点A与点E重合、点B与点D重合,写出一种变化的过程_____.
,对应的坐标如下,请利用学过的变换(平移、旋转、轴对称)知识经过若干次图形变化,使得点A与点E重合、点B与点D重合,写出一种变化的过程_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明每天早上要到距家1000米的学校上学,一天,小明以80米/分钟的速度出发,5分钟后,小明的爸爸发现他忘带了数学书,于是,爸爸立即以180米/分钟的速度去追赶小明.
(1)若爸爸在途中追上了小明,请问爸爸追上小明用了多长时间?
(2)若爸爸出发2分钟后,小明也发现自己忘带数学书,于是他以100米/分钟往回走,与爸爸在途中相遇了,请问这种情况下爸爸出发多久追上小明?
(3)小明家养了一条聪明伶俐的小狗,小狗跟着爸爸冲出了门,以240米/分钟的速度去追小明,小明看到小狗的一刹那醒悟到自己忘了带数学书,立即以120米/分钟的速度往回返,小狗仍以原速度往爸爸这边跑,跑到爸爸身边又折回往小明身边跑,直到爸爸和小明相遇方停下,随后又跟着爸爸回到家,请问小狗从出门到回家共跑了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初二年级教师对试卷讲评课中学生参与的深度与广度进行评价调查,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初二学生的参与情况,绘制成如图所示的频数分布直方图和扇形统计图(均不完整),请根据图中所给信息解答下列问题:
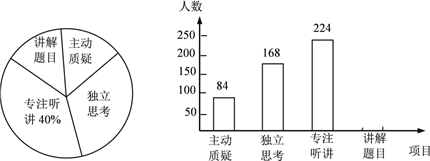
(1)在这次评价中,一共抽查了 名学生;
(2)在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为 度;
(3)请将频数分布直方图补充完整;
(4)如果全市有6000名初二学生,那么在试卷评讲课中,“独立思考”的初二学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(1,2)为反比例函数![]() 图象上一点,
图象上一点,
(1) 将点A沿x轴正方向平移1个单位,对应点A′的坐标为___________
将比例函数![]() 图象沿x轴正方向平移1个单位,平移后的函数解析式为___________
图象沿x轴正方向平移1个单位,平移后的函数解析式为___________
将比例函数![]() 图象沿x轴正方向平移m个单位,平移后的函数解析式为___________
图象沿x轴正方向平移m个单位,平移后的函数解析式为___________
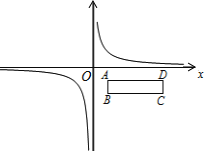
(2) 在平面直角坐标系中,矩形ABCD位置如图,其中A、B、C三点的坐标分别为A(1,-1)、B(1,-2)、C(4,-2).现将反比例函数![]() 图象沿x轴正方向平移,若平移速度为每秒1个单位长度
图象沿x轴正方向平移,若平移速度为每秒1个单位长度
① 设函数图象平移时间为t秒,求函数图象与矩形ABCD有公共点时t的取值范围;
② 在平移过程中,当函数图象与矩形ABCD有公共点时,则函数图象扫过的区域夹在直线AD、BC的图形面积为___________(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新定义:[a,b,c]为二次函数y=ax2+bx+e(a≠0,a,b,c为实数)的“图象数”,如:y=-x2+2x+3的“图象数”为[-1,2,3]
(1)二次函数y=![]() x2-x-1的“图象数”为 .
x2-x-1的“图象数”为 .
(2)若图象数”是[m,m+1,m+1]的二次函数的图象与x轴只有一个交点,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=8,BC=6.CD⊥AB于点D.点P从点A出发,以每秒1个单位长度的速度沿线段AB向终点B运动.在运动过程中,以点P为顶点作长为2,宽为1的矩形PQMN,其中PQ=2,PN=1,点Q在点P的左侧,MN在PQ的下分,且PQ总保持与AC垂直.设P的运动时间为t(秒)(t>0),矩形PQMN与△ACD的重叠部分图形面积为S(平方单位).
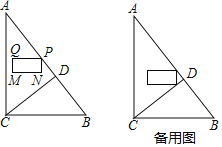
(1)求线段CD的长;
(2)当矩形PQMN与线段CD有公共点时,求t的取值范围;
(3)当点P在线段AD上运动时,求S与t的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料:思考的同学小斌在解决连比等式问题:“已知正数![]() ,
,![]() ,
,![]() 满足
满足![]() ,求
,求![]() 的值”时,采用了引入参数法
的值”时,采用了引入参数法![]() ,将连比等式转化为了三个等式,再利用等式的基本性质求出参数的值.进而得出
,将连比等式转化为了三个等式,再利用等式的基本性质求出参数的值.进而得出![]() ,
,![]() ,
,![]() 之间的关系,从而解决问题.过程如下:
之间的关系,从而解决问题.过程如下:
解;设![]() ,则有:
,则有:
![]() ,
,![]() ,
,![]() ,
,
将以上三个等式相加,得![]() .
.
![]()
![]() ,
,![]() ,
,![]() 都为正数,
都为正数,
![]()
![]() ,即
,即![]() ,.
,.
![]()
![]() .
.
仔细阅读上述材料,解决下面的问题:
(1)若正数![]() ,
,![]() ,
,![]() 满足
满足![]() ,求
,求![]() 的值;
的值;
(2)已知![]() ,
,![]() ,
,![]() ,
,![]() 互不相等,求证:
互不相等,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com