
����Ŀ��С��ÿ������Ҫ�����1000��ѧУ��ѧ��һ�죬С����80��/���ӵ��ٶȳ�����5���Ӻ�С���İְַ�������������ѧ�飬���ǣ��ְ�������180��/���ӵ��ٶ�ȥ��С����
��1�����ְ���;������С�������ʰְ���С�����˶ʱ�䣿
��2�����ְֳ���2���Ӻ�С��Ҳ�����Լ�������ѧ�飬��������100��/���������ߣ���ְ���;�������ˣ�������������°ְֳ��������С����
��3��С��������һ������������С����С�����Űְֳ�����ţ���240��/���ӵ��ٶ�ȥС����С������С����һɲ�������Լ����˴���ѧ�飬������120��/���ӵ��ٶ����ط���С������ԭ�ٶ����ְ�����ܣ��ܵ��ְ��������ۻ���С�������ܣ�ֱ���ְֺ�С��������ͣ�£�����ָ��Űְֻص��ң�����С���ӳ��ŵ��ؼҹ����˶����ף�
���𰸡���1���ְ���С������4���ӣ���2���ְֳ���![]() ������С������3��С���ӳ��ŵ��ؼҹ�����1260�ף�
������С������3��С���ӳ��ŵ��ؼҹ�����1260�ף�
��������
��1���������������⣬�������Ļ���������ϵ������ʽ��⼴�ɵý⣻
��2������������֣��ְֳ�����ǰ2����Ϊ�����⣬����ڶ�����Ϊ�������������ʽ���㼴�ɵý⣻
��3���������⣬��С����ְֵ�����ʱ�����С�����ٶȼ��ɵõ�С������ʻ·��.
��1����С���ְ���С������x���ӣ�������ã�
![]() ��
��
���x��4��
�𣺰ְ���С������4���ӣ�
��2����ְֳ���y������С����������ã�
![]() ��
��
���![]() ��
��
�𣺰ְֳ���![]() ������С����
����������
��3��![]() ���֣���
���֣���
![]() ���֣���
���֣���
![]() ���ף���
���ף���
��С���ӳ��ŵ��ؼҹ�����1260�ף�


 �������Ͽ��㱾ϵ�д�
�������Ͽ��㱾ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��ͬѧ��һ����Ǯ���˱������������ijһ�ܳ�ʼ��ǮΪ100Ԫ����һ���������֧������£�������Ϊ+����λ��Ԫ����
+25��-15.5��-23��-17��+26
��1������ĩ������֧�����ǮΪ��Ԫ��
��2��������������![]() Ԫ����2���飬�������ְָ�����10Ԫ���緹������ʵ������15Ԫ��ǡ�����������е���Ǯ����
Ԫ����2���飬�������ְָ�����10Ԫ���緹������ʵ������15Ԫ��ǡ�����������е���Ǯ����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AOBC�Ķ���O��0��0����A����1��2������B��x���������ϰ����²�����ͼ�����Ե�OΪԲ�ģ��ʵ�����Ϊ�뾶�������ֱ�OA��OB�ڵ�D��E���ڷֱ��Ե�D��EΪԲ�ģ�����![]() DE�ij�Ϊ�뾶�����������ڡ�AOB�ڽ��ڵ�F����������OF������AC�ڵ�G�����G������Ϊ��������
DE�ij�Ϊ�뾶�����������ڡ�AOB�ڽ��ڵ�F����������OF������AC�ڵ�G�����G������Ϊ��������
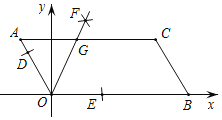
A. ��![]() ��1��2�� B. ��
��1��2�� B. ��![]() ��2�� C. ��3��
��2�� C. ��3��![]() ��2�� D. ��
��2�� D. ��![]() ��2��2��
��2��2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪:��ͼ��![]() �ֱ�Ϊ����( ��С���ᷢ���ı�)
�ֱ�Ϊ����( ��С���ᷢ���ı�) ![]() �ڲ������������ߣ�
�ڲ������������ߣ�

��1����![]() �˶�����ͼ1��λ��ʱ��
�˶�����ͼ1��λ��ʱ��![]() ����
����![]() �Ķ�����
�Ķ�����
��2����(1)��������(ͼ2)������![]() �ֱ�Ϊ
�ֱ�Ϊ![]() ��ƽ���ߣ���
��ƽ���ߣ���![]() �Ķ�����
�Ķ�����
��3����(1)��������(ͼ3)��![]() ��
��![]() �ⲿ���������ߣ�
�ⲿ���������ߣ�![]() ��
��![]() ƽ��
ƽ��![]() ��
��![]() ƽ��
ƽ��![]() ����
����![]() �Ķ�����
�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��������AN��ȡһ��B��ʹ
��������AN��ȡһ��B��ʹ![]() ������
������![]() ��
��![]() �ڵ�C����D���߶�AB�ϵ�һ�����㣬E��BC����һ�㣬��
�ڵ�C����D���߶�AB�ϵ�һ�����㣬E��BC����һ�㣬��![]() ,��AD=x cm��BE=y cm��̽������y���Ա���x�ı仯���仯�Ĺ���.
,��AD=x cm��BE=y cm��̽������y���Ա���x�ı仯���仯�Ĺ���.

��1��ȡָ������ͼ.�����������Ԥ��������ͨ����ͼȷ��AD=2cmʱ����E��λ�ã�����BE�ij��ȡ�
�ٸ������⣬���������ȫͼ�Σ�
�ڰѱ���������ͨ��ȡ�㡢��ͼ���������õ���![]() ��
��![]() �ļ����Ӧֵ�����±���
�ļ����Ӧֵ�����±���
|
|
| 2 | 3 |
|
|
|
| 2.9 | 3.4 | 3.3 | 2.6 | 1.6 | 0 |
��˵������ȫ����ʱ�����ֵ����һλС����
������ƽ��ֱ������ϵ������Բ�ȫ��ı��и��Զ�ӦֵΪ����ĵ㣬�����ú�����ͼ����

��2����ϻ����ĺ���ͼ������⣺��![]() ʱ��
ʱ��![]() ��ȡֵԼΪ__________
��ȡֵԼΪ__________![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=8��AC=6����D�ڱ�AB�ϣ�AD=4.5����ABC�Ľ�ƽ����AE��CD�ڵ�F��
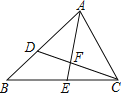
��1����֤����ACD�ס�ABC��
��2����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��ˮ���г�ijƷ��ƻ�������۷�ʽ���±���
����ƻ������ǧ�ˣ� | ������ | ���� |
ÿǧ�˵ļ۸�Ԫ�� |
|
|
��1�����С������![]() ǧ�˵�ƻ������ô����Ҫ��___________Ԫ��
ǧ�˵�ƻ������ô����Ҫ��___________Ԫ��
��2��С�������ι�����![]() ǧ�˵�ƻ�����ڶ��ι�����������ڵ�һ�ι�����������������ι���
ǧ�˵�ƻ�����ڶ��ι�����������ڵ�һ�ι�����������������ι���![]() Ԫ���������ηֱ���ƻ����������
Ԫ���������ηֱ���ƻ����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������۰Ĵ���������ļ����ƽ����㶫ʡ�����ٲ�����5G��Ϊ������ս�������˲�ҵ����ͳ�ƣ�Ŀǰ�㶫5G��վ������Լ1.5�������ƻ���2020��ף�ȫʡ5G��վ����Ŀǰ��4������2022��ף�ȫʡ5G��վ�������ﵽ17.34������
��1���ƻ���2020��ף�ȫʡ5G��վ�������Ƕ�����������
��2�����ռƻ�����2020���2022��ף�ȫʡ5G��վ��������ƽ�������ʡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() �ֱ�ֱ��
�ֱ�ֱ��![]() ��
��![]() ��
��![]() ��
��![]() ���㣬����
���㣬����![]() ��
��![]() ��ֱ��
��ֱ��![]() �ڵ�
�ڵ�![]() ����
����![]() ��ֱ��
��ֱ��![]() ��һ�㣬����
��һ�㣬����![]() ����֪
����֪![]() ��
��
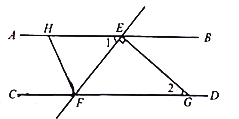
��1����֤��![]() ��
��
��2����![]() ��
��![]() ƽ��
ƽ��![]() ����
����![]() �Ķ�����
�Ķ�����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com