
【题目】已知:如图,![]() 分别为定角( 大小不会发生改变)
分别为定角( 大小不会发生改变) ![]() 内部的两条动射线,
内部的两条动射线,

(1)当![]() 运动到如图1的位置时,
运动到如图1的位置时,![]() ,求
,求![]() 的度数.
的度数.
(2)在(1)的条件下(图2),射线![]() 分别为
分别为![]() 的平分线,求
的平分线,求![]() 的度数.
的度数.
(3)在(1)的条件下(图3),![]() 是
是![]() 外部的两条射线,
外部的两条射线,![]() ,
,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,求
,求![]() 的度数.
的度数.
【答案】(1)∠AOD=70°;(2)∠MON=50°;(3)∠POQ=110°.
【解析】
(1)根据角的定义可以得出∠AOC+∠BOD=∠AOB+∠COD+2∠BOC,然后可先求出∠BOC,最后再进一步求解即可;
(2)利用角平分线性质进一步求解即可;
(3)根据题意先求出∠POD+∠AOQ的值,然后再进一步求解即可.
(1)∵∠AOC+∠BOD=100°,∠AOB+∠COD=40°,
又∵∠AOC+∠BOD=∠AOB+∠COD+2∠BOC,
∴40°+ 2∠BOC=100°,
∴∠BOC=30°,
∴∠AOD=∠BOC+∠AOB+∠COD=70° ;
(2)∵OM、ON分别为∠AOB、∠COD的平分线,
∴∠CON+∠BOM=![]() (∠AOB+∠COD)=
(∠AOB+∠COD)=![]() ×40°=20°,
×40°=20°,
∴∠MON=∠CON+∠BOM+∠BOC=20°+30°=50°;
(3)∵OP平分∠EOD, OQ平分∠AOF,
∴∠POD+∠AOQ =![]() (∠EOD+∠AOF),
(∠EOD+∠AOF),
∵∠EOD=∠EOB∠BOD=90°∠BOD,
同理,∠AOF = 90°∠AOC,
∴∠EOD+∠AOF=180°∠BOD +∠AOC)=180°100°=80°,
∴∠POD+∠AOQ =![]() (∠EOD+∠AOF)=40°,
(∠EOD+∠AOF)=40°,
∴∠POQ=∠POD+∠AOQ+∠AOD=40°+70°=110°.


科目:初中数学 来源: 题型:
【题目】某学校为了开展“阳光体育运动”,计划购买篮球与足球共![]() 个,已知每个篮球的价格为
个,已知每个篮球的价格为![]() 元,每个足球的价格为
元,每个足球的价格为![]() 元
元
(1)若购买这两类球的总金额为![]() 元,求篮球和足球各购买了多少个?
元,求篮球和足球各购买了多少个?
(2)元旦期间,商家给出蓝球打九折,足球打八五折的优惠价,若购买这种篮球与足球各![]() 个,那么购买这两类球一共需要多少钱?
个,那么购买这两类球一共需要多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某书店准备购进甲、乙两种图书共100本,购书款不高于2224元,两种图书的进价、售价如下表所示:
甲种图书 | 乙种图书 | |
进价(元/本) | 16 | 28 |
售价(元/本) | 26 | 40 |
请解答下列问题:
(1)在这批图书全部售出的条件下,书店如何进货利润最大?最大利润是多少?
(2)书店计划用(1)中的最大利润购买单价分别为72元、96元的排球、篮球捐给贫困山区的学校,那么在钱恰好用尽的情况下,最多可以购买排球和篮球共多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平行四边形![]() 中,点
中,点![]() 是对角线
是对角线![]() 的中点,
的中点,![]() 过点
过点![]() 与
与![]() ,
,![]() 分别相交于
分别相交于![]() ,
,![]() ,
,![]() 过点
过点![]() 与
与![]() ,
,![]() 分别相交于点
分别相交于点![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)如图2,若![]() ,
,![]() ,在不添加任何辅助的情况下,请直接写出图2中与四边形
,在不添加任何辅助的情况下,请直接写出图2中与四边形![]() 面积相等的所有的平行四边形(四边形
面积相等的所有的平行四边形(四边形![]() 除外).
除外).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知![]() ,对应的坐标如下,请利用学过的变换(平移、旋转、轴对称)知识经过若干次图形变化,使得点A与点E重合、点B与点D重合,写出一种变化的过程_____.
,对应的坐标如下,请利用学过的变换(平移、旋转、轴对称)知识经过若干次图形变化,使得点A与点E重合、点B与点D重合,写出一种变化的过程_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“朗读者”节目的影响下,某中学在暑期开展了“好书伴我成长”读书话动,并要求读书要细读,最少要读完2本书,最多不建议超过5本。初一年级5个班,共200名学生,李老师为了了解学生暑期在家的读书情况,给全班同学布置了一项调查作业:了解初一年级学生暑期读书情况.班中三位同学各自对初一年级读书情况进行了抽样调查,并将数据进行了整理,绘制的统计图表分别为表1、表2、表3.
表1:在初一年级随机选择5名学生暑期读书情况的统计表
阅读书数量(本) | 2 | 3 | 4 | 5 |
人数 | 2 | 1 | 1 | 1 |
表2:在初一年级“诵读班”班随机选取20名学生暑期读书情况的统计表
阅读书数量(本) | 2 | 3 | 4 | 5 |
人数 | 0 | 1 | 4 | 15 |
表3:在初一年级随机选取20名学生暑期读书情况的统计表
阅读书数量(本) | 2 | 3 | 4 | 5 |
人数 | 2 | 8 | 6 | 4 |
问题1:根据以上材料回答:三名同学中,哪一位同学的样本选取更合理,并简要说明其他两位同学选取样本的不足之处;
老师又对合理样本中的所有学生进行了“阅读动机”的调研,并制作成了如下统计图.
问题2:通过统计图的信息你认为“阅读动机”
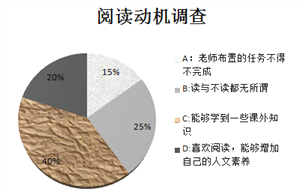
在“40%”的群体,暑期读几本书的可能性大,并说出你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明每天早上要到距家1000米的学校上学,一天,小明以80米/分钟的速度出发,5分钟后,小明的爸爸发现他忘带了数学书,于是,爸爸立即以180米/分钟的速度去追赶小明.
(1)若爸爸在途中追上了小明,请问爸爸追上小明用了多长时间?
(2)若爸爸出发2分钟后,小明也发现自己忘带数学书,于是他以100米/分钟往回走,与爸爸在途中相遇了,请问这种情况下爸爸出发多久追上小明?
(3)小明家养了一条聪明伶俐的小狗,小狗跟着爸爸冲出了门,以240米/分钟的速度去追小明,小明看到小狗的一刹那醒悟到自己忘了带数学书,立即以120米/分钟的速度往回返,小狗仍以原速度往爸爸这边跑,跑到爸爸身边又折回往小明身边跑,直到爸爸和小明相遇方停下,随后又跟着爸爸回到家,请问小狗从出门到回家共跑了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
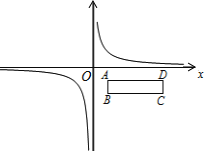
【题目】已知点A(1,2)为反比例函数![]() 图象上一点,
图象上一点,
(1) 将点A沿x轴正方向平移1个单位,对应点A′的坐标为___________
将比例函数![]() 图象沿x轴正方向平移1个单位,平移后的函数解析式为___________
图象沿x轴正方向平移1个单位,平移后的函数解析式为___________
将比例函数![]() 图象沿x轴正方向平移m个单位,平移后的函数解析式为___________
图象沿x轴正方向平移m个单位,平移后的函数解析式为___________
(2) 在平面直角坐标系中,矩形ABCD位置如图,其中A、B、C三点的坐标分别为A(1,-1)、B(1,-2)、C(4,-2).现将反比例函数![]() 图象沿x轴正方向平移,若平移速度为每秒1个单位长度
图象沿x轴正方向平移,若平移速度为每秒1个单位长度
① 设函数图象平移时间为t秒,求函数图象与矩形ABCD有公共点时t的取值范围;
② 在平移过程中,当函数图象与矩形ABCD有公共点时,则函数图象扫过的区域夹在直线AD、BC的图形面积为___________(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境
在综合与实践课上,老师让同学们以“两条平行线AB,CD和一块含60°角的直角三角尺EFG(∠EFG=90°,∠EGF=60°)”为主题开展数学活动.
操作发现
(1)如图(1),小明把三角尺的60°角的顶点G放在CD上,若∠2=2∠1,求∠1的度数;
(2)如图(2),小颖把三角尺的两个锐角的顶点E、G分别放在AB和CD上,请你探索并说明∠AEF与∠FGC之间的数量关系;
结论应用
(3)如图(3),小亮把三角尺的直角顶点F放在CD上,30°角的顶点E落在AB上.若∠AEG=α,则∠CFG等于______(用含α的式子表示).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com