
【题目】如图,直线![]() 分别交直线
分别交直线![]() ,
,![]() 于
于![]() ,
,![]() 两点,过点
两点,过点![]() 作
作![]() 交直线
交直线![]() 于点
于点![]() ,点
,点![]() 是直线
是直线![]() 上一点,连接
上一点,连接![]() ,已知
,已知![]() .
.
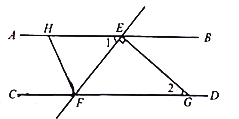
(1)求证:![]() ;
;
(2)若![]() ,
,![]() 平分
平分![]() ,求
,求![]() 的度数.
的度数.
科目:初中数学 来源: 题型:
【题目】小明每天早上要到距家1000米的学校上学,一天,小明以80米/分钟的速度出发,5分钟后,小明的爸爸发现他忘带了数学书,于是,爸爸立即以180米/分钟的速度去追赶小明.
(1)若爸爸在途中追上了小明,请问爸爸追上小明用了多长时间?
(2)若爸爸出发2分钟后,小明也发现自己忘带数学书,于是他以100米/分钟往回走,与爸爸在途中相遇了,请问这种情况下爸爸出发多久追上小明?
(3)小明家养了一条聪明伶俐的小狗,小狗跟着爸爸冲出了门,以240米/分钟的速度去追小明,小明看到小狗的一刹那醒悟到自己忘了带数学书,立即以120米/分钟的速度往回返,小狗仍以原速度往爸爸这边跑,跑到爸爸身边又折回往小明身边跑,直到爸爸和小明相遇方停下,随后又跟着爸爸回到家,请问小狗从出门到回家共跑了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=8,BC=6.CD⊥AB于点D.点P从点A出发,以每秒1个单位长度的速度沿线段AB向终点B运动.在运动过程中,以点P为顶点作长为2,宽为1的矩形PQMN,其中PQ=2,PN=1,点Q在点P的左侧,MN在PQ的下分,且PQ总保持与AC垂直.设P的运动时间为t(秒)(t>0),矩形PQMN与△ACD的重叠部分图形面积为S(平方单位).
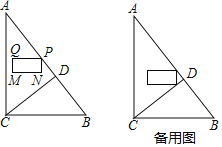
(1)求线段CD的长;
(2)当矩形PQMN与线段CD有公共点时,求t的取值范围;
(3)当点P在线段AD上运动时,求S与t的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境
在综合与实践课上,老师让同学们以“两条平行线AB,CD和一块含60°角的直角三角尺EFG(∠EFG=90°,∠EGF=60°)”为主题开展数学活动.
操作发现
(1)如图(1),小明把三角尺的60°角的顶点G放在CD上,若∠2=2∠1,求∠1的度数;
(2)如图(2),小颖把三角尺的两个锐角的顶点E、G分别放在AB和CD上,请你探索并说明∠AEF与∠FGC之间的数量关系;
结论应用
(3)如图(3),小亮把三角尺的直角顶点F放在CD上,30°角的顶点E落在AB上.若∠AEG=α,则∠CFG等于______(用含α的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一张长方形纸片![]() (如图①),
(如图①),![]() ,将纸片折叠,使
,将纸片折叠,使![]() 落在
落在![]() 边上,
边上,![]() 为
为![]() 的对应点,折痕为
的对应点,折痕为![]() (如图②),再将长方形
(如图②),再将长方形![]() 以
以![]() 为折痕向右折叠,若点
为折痕向右折叠,若点![]() 落在
落在![]() 的三等分点上,则
的三等分点上,则![]() 的长为( )
的长为( )

A.8B.10C.8或10D.8或12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知坐标平面内的三个点![]() ,
,![]() ,
,![]() ,把
,把![]() 向下平移
向下平移![]() 个单位再向右平移
个单位再向右平移![]() 个单位后得到
个单位后得到![]() .
.
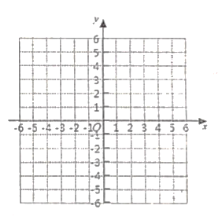
(1)直接写出![]() ,
,![]() ,
,![]() 三个对应点
三个对应点![]() 、
、![]() 、
、![]() 的坐标;
的坐标;
(2)画出将![]() 绕
绕![]() 点逆时针方向旋转
点逆时针方向旋转![]() 后得到
后得到![]() ;
;
(3)求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料:思考的同学小斌在解决连比等式问题:“已知正数![]() ,
,![]() ,
,![]() 满足
满足![]() ,求
,求![]() 的值”时,采用了引入参数法
的值”时,采用了引入参数法![]() ,将连比等式转化为了三个等式,再利用等式的基本性质求出参数的值.进而得出
,将连比等式转化为了三个等式,再利用等式的基本性质求出参数的值.进而得出![]() ,
,![]() ,
,![]() 之间的关系,从而解决问题.过程如下:
之间的关系,从而解决问题.过程如下:
解;设![]() ,则有:
,则有:
![]() ,
,![]() ,
,![]() ,
,
将以上三个等式相加,得![]() .
.
![]()
![]() ,
,![]() ,
,![]() 都为正数,
都为正数,
![]()
![]() ,即
,即![]() ,.
,.
![]()
![]() .
.
仔细阅读上述材料,解决下面的问题:
(1)若正数![]() ,
,![]() ,
,![]() 满足
满足![]() ,求
,求![]() 的值;
的值;
(2)已知![]() ,
,![]() ,
,![]() ,
,![]() 互不相等,求证:
互不相等,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某市2018年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图.
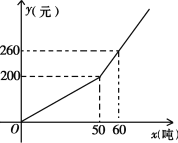
(1)当x≥50时,求y关于x的函数关系式;
(2)若某企业2018年10月份的水费为620元,求该企业2018年10月份的用水量.
查看答案和解析>>
科目:初中数学 来源: 题型:
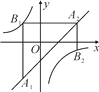
【题目】如图,已知点A1,A2,…,An均在直线y=x-1上,点B1,B2,…,Bn均在双曲线y=-![]() 上,并且满足A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=-1,则a2018=_______.
上,并且满足A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=-1,则a2018=_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com